查找
顺序查找
按照顺序一个个比较,直到序列末尾
int seq_search(int array[], int n, int key)
{
int i;
for(i = 0; i < n; i++)
{
if(key == array[i])
{
return i; //查找成功
}
}
return -1; //查找失败
}
二分查找
通过对一个有序数组中对元素依次比较,从而能实现对数级别时间复杂度的查找
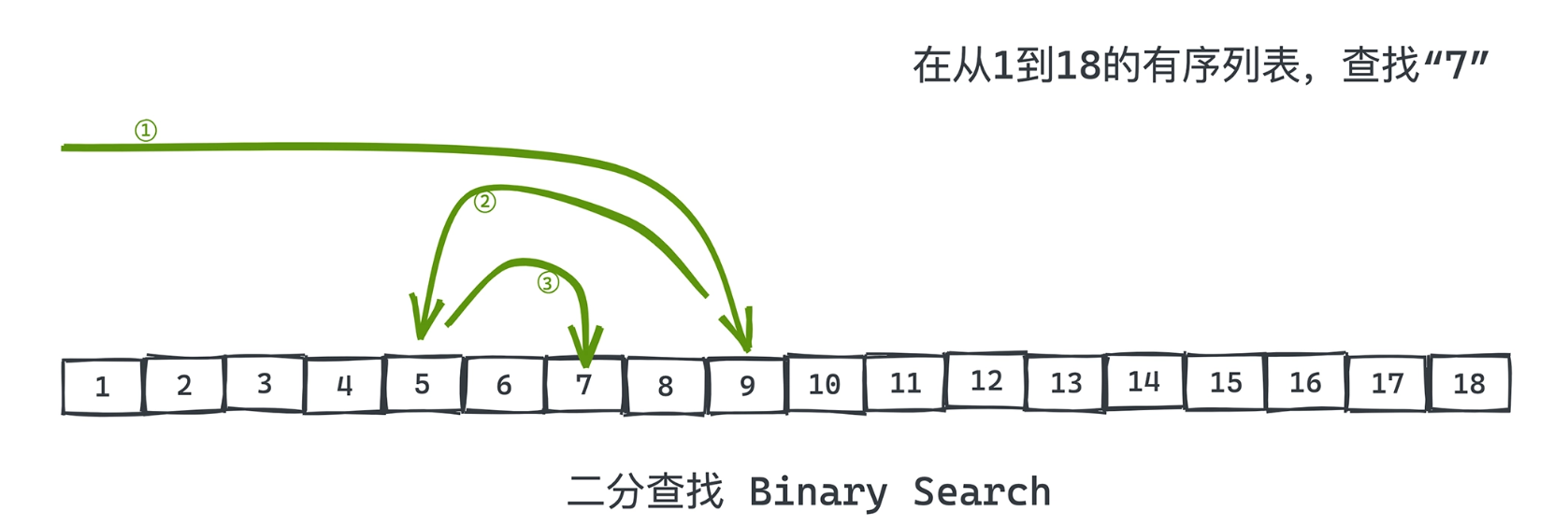
根据左右指针计算出一个mid指针 如果mid指针处的元素等于目标值 则要查找的目标就是在这里
否则如果mid处的指针比目标值大 则右指针等于mid-1 否则左指针等于mid+1
然后重复上述操作 直到左指针大于右指针
int l = 0, r = a.length - 1;
while (l <= r) {
int mid = l + (r - l) / 2;
if (a[mid].equals(target)) {
return mid;
}
if (less(target, a[mid])) {// 要查找的元素在左边
r = mid - 1;
} else if (greater(target, a[mid])) { // 要查找的元素在右边
l = mid + 1;
}
}
return -1;
这个算法在快速定位BUG的时候也挺好用,一分为二,确定问题在前端还是后端,再继续划分,确定问题在系统哪一层
二叉查找树
- 擅长数据的查找
- 高效
特点
每个结点的键值大于左孩子,小于右孩子
每个孩子又是二叉查找树
二分查找树不一定是完全二叉树
对于任何节点:
- 左子树上所有节点都小于它
- 右子树所有节点都大于它
插入
if (root == null) {
count++;
return new Node(key, value); // 当前节点为null,则创建一个节点返回
}
if (key.equals(root.key)) { // 当前节点等于要插入的节点,则直接覆盖
root.value = value;
} else if (less(key, root.key)) { // 当前节点比要插入的大,则向当前节点的左子树插入
root.left = insert(root.left, key, value);
} else if (greater(key, root.key)) { // 当前节点比要插入的小,则向当前节点的右子树插入
root.right = insert(root.right, key, value);
}
查找
原理同插入,根据左子树比父节点小,右子树比父节点大的条件
if (root == null){
return null;
}
if (key.equals(root.key)){
return root.value;
}else if(less(key,root.key)){
return search(root.left,key);
}else {
return search(root.right,key);
}
floor与ceil
- floor:是最接近key值且小于key的节点
- ceil:是最接近key值且大于key的节点
遍历
- 前序遍历
先访问当前节点,再递归访问左右子树
if (root != null){
consumer.accept(root.key,root.value);
preOrder(root.left,consumer);
preOrder(root.right,consumer);
}
- 中序遍历
先递归访问左子树,再访问自身,再递归访问右子树
if (root != null){
preOrder(root.left,consumer);
consumer.accept(root.key,root.value);
preOrder(root.right,consumer);
}
- 后序遍历
先递归访问左右子树,在访问自身
if (root != null){
preOrder(root.left,consumer);
preOrder(root.right,consumer);
consumer.accept(root.key,root.value);
}
- 广度优先遍历(层序)
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
var node = queue.remove();
consumer.accept(node.key,node.value);
if (node.left != null){
queue.add(node.left);
}
if (node.right != null){
queue.add(node.right);
}
}
删除
分为三种情况
删除叶子节点
- 直接解除父节点对其的引用即可
删除只有一个子节点的
- 将父节点指向其子节点
private Node removeMax(Node node) {
if (node.right == null) {
// 代表当前节点就是最大节点,所以返回当前节点的左子树给父节点
count--;
return node.left;
}
// 将删除的节点的左子树作为父节点的右子树
node.right = removeMax(node.right);
return node;
}
- 删除有两个子节点的
Hubbard Deletion
使用被删除节点右子树中的最小节点来代替被删除节点
局限性
- 同样的数据会对应不同的查找树
- 查找树随着数据的不断增加或插入容易失衡,退化成链表
平衡二叉树
- 树及其子树的左右高度差不能超过1
- 空树及只有根节点的树也是平衡二叉树
AVL树
在增加和删除节点时通过旋转来保持平衡
右旋:以某个节点为中心 将它沉入当前右子节点的位置 然后让当前左子节点作为新树的根
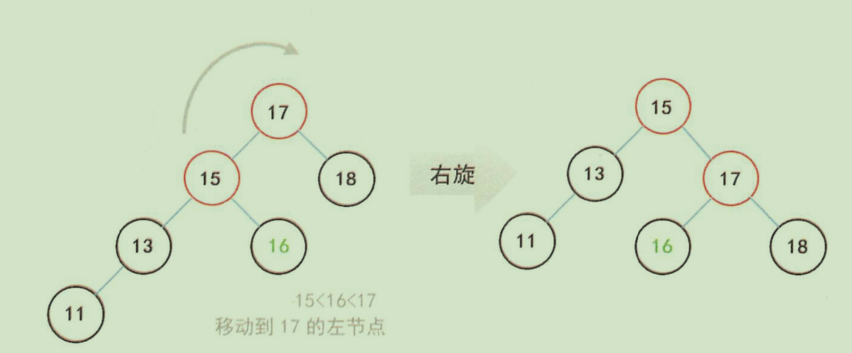
左旋:
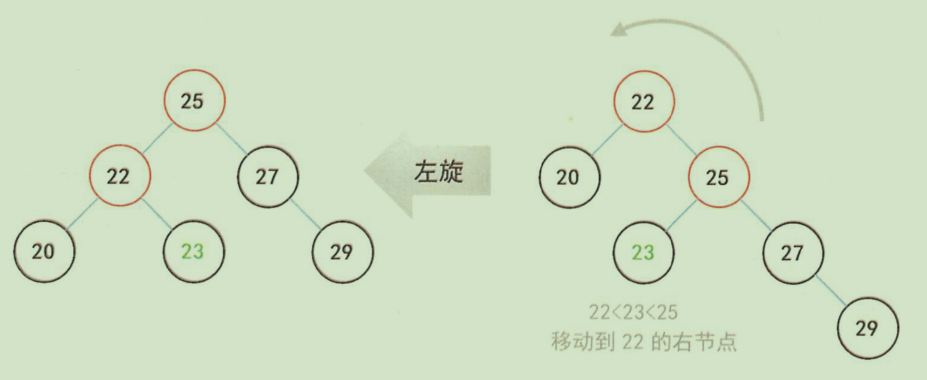
2-3查找树
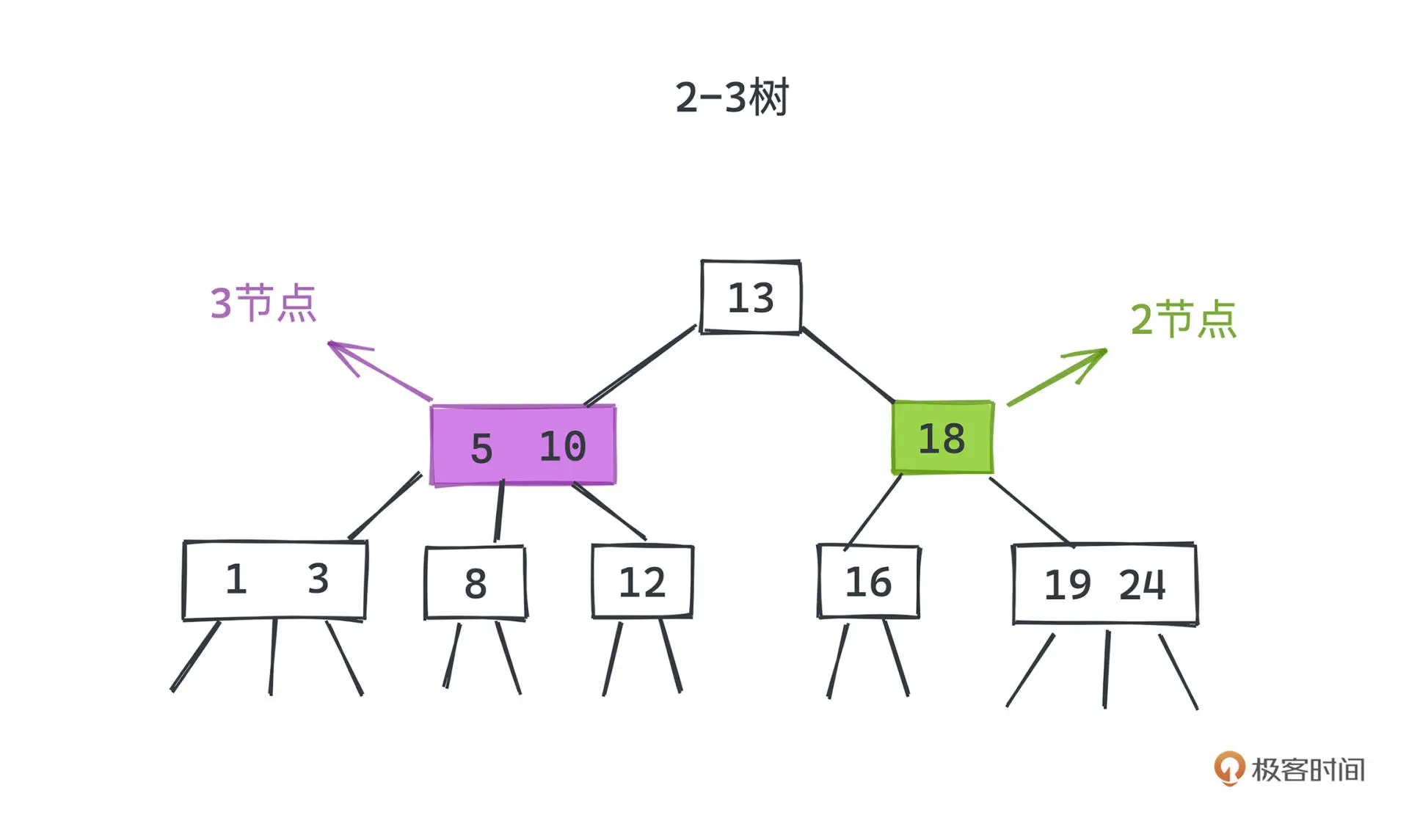
搜索
搜索的过程和二叉树并没有太多的区别,只是遇到 3 节点的时候,多判断一次是否介于 a、b 之间
插入
2-3树之所以完美平衡,关键在于插入时的维护
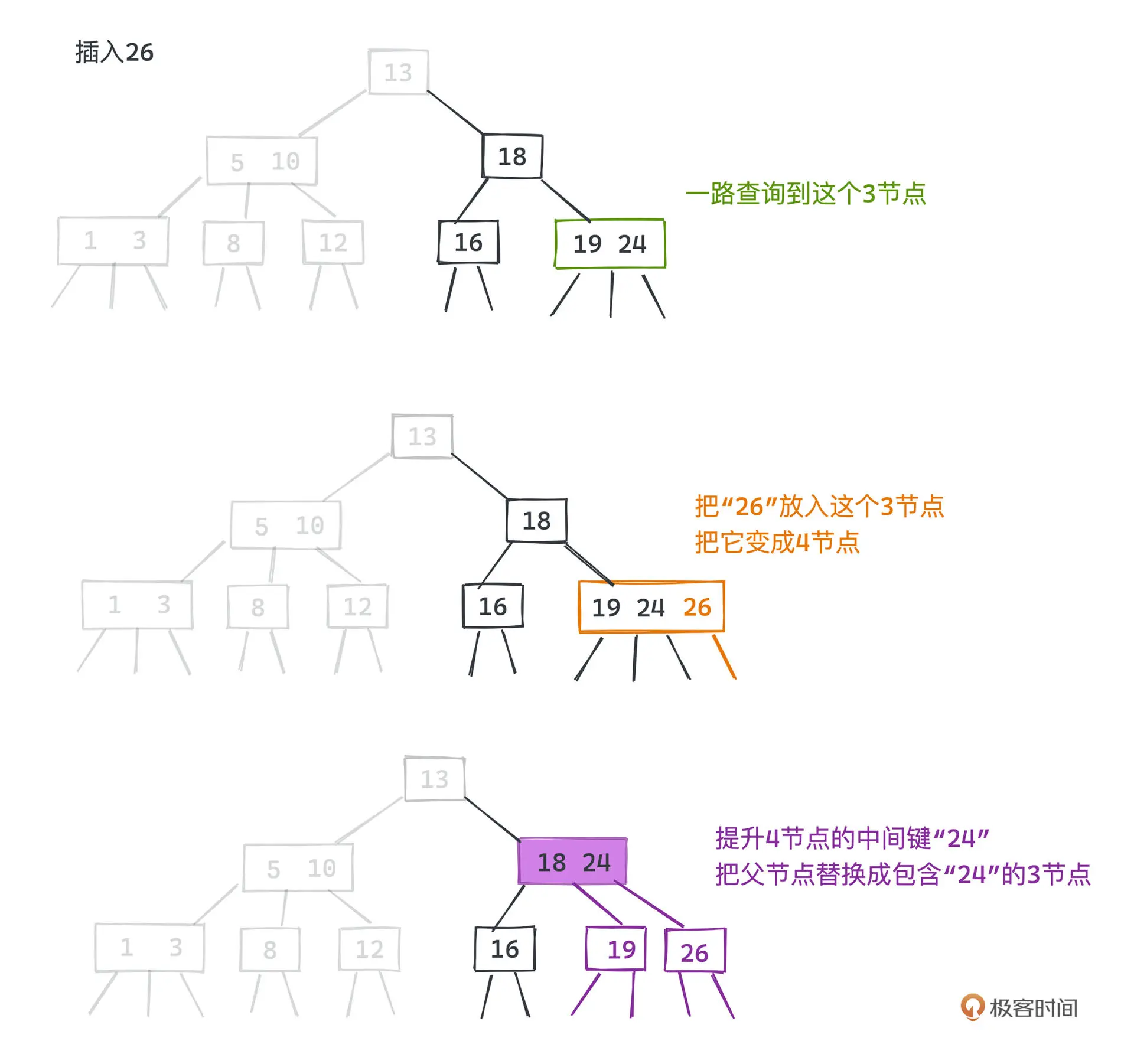
删除
红黑树
红黑树,正是采用标准的二叉查找树节点附着上额外的颜色信息来表示 2-3 树的实现,每一个红色节点都和它的父亲节点一起,构成了一个 3 节点的模拟,通过旋转操作完成 2-3 节点的合并和分裂,从而在不改变二叉树节点结构的前提下,保证二叉树的有序性和平衡性
红黑树不追求左右子树高度差不超过1
而是保证从根节点到叶尾的最长路径不超过最短路径的2倍
其他约束条件:
- 节点只能是红色或者黑色
- 根节点必须是黑色
- NIL(Nothing in leaf)节点都是黑色
- 相连的两个节点不能都是红色
- 根节点到叶子节点的所有路径黑色节点数量都相同
红黑树的任何旋转至多3次就能完成
这些约束,都是为了保证每一颗红黑树和 2-3 Tree 是一一对应的
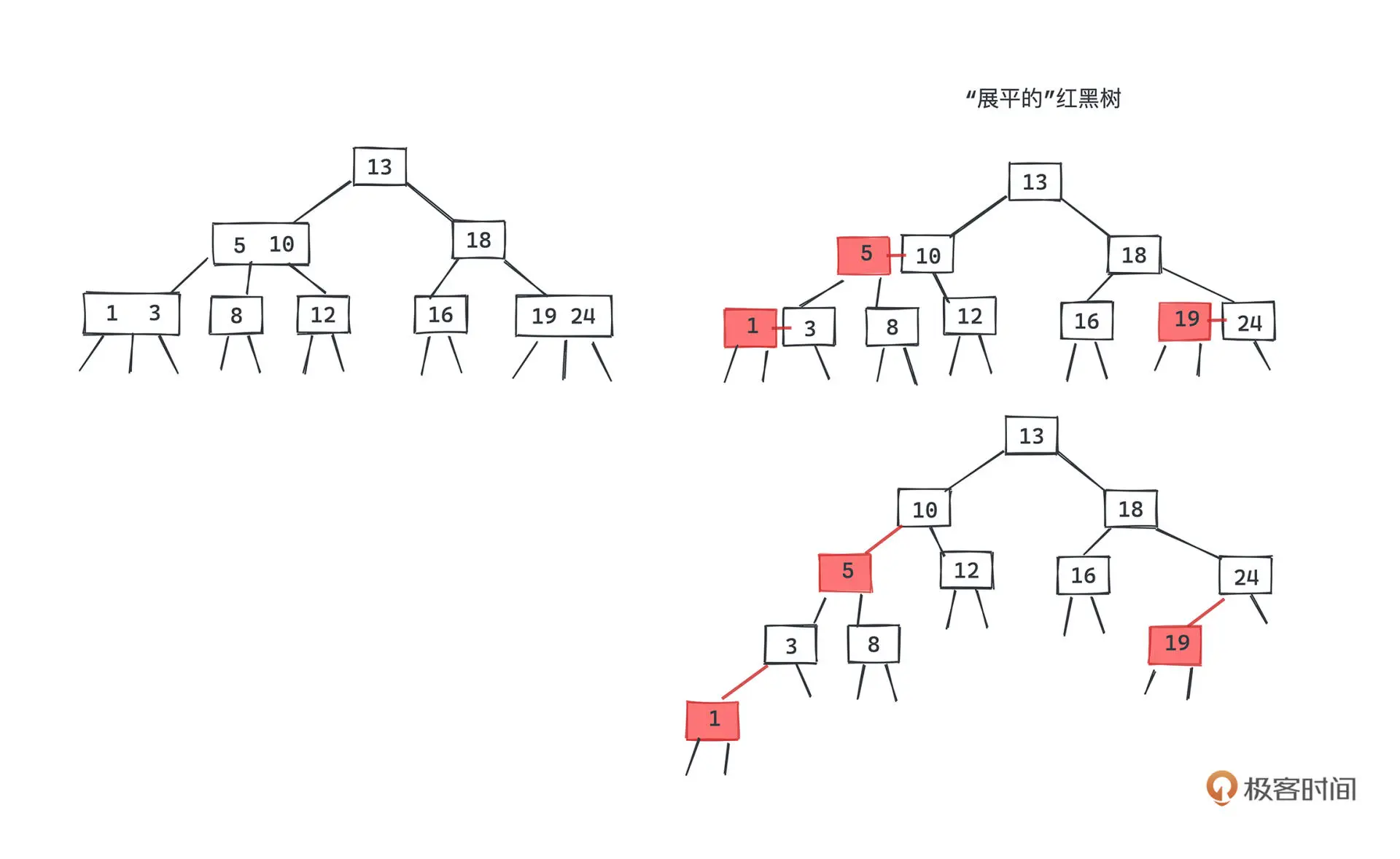
基本操作
旋转
左旋:本质上就是将某个 3 节点从以较小的键为根转移成较大的键为根
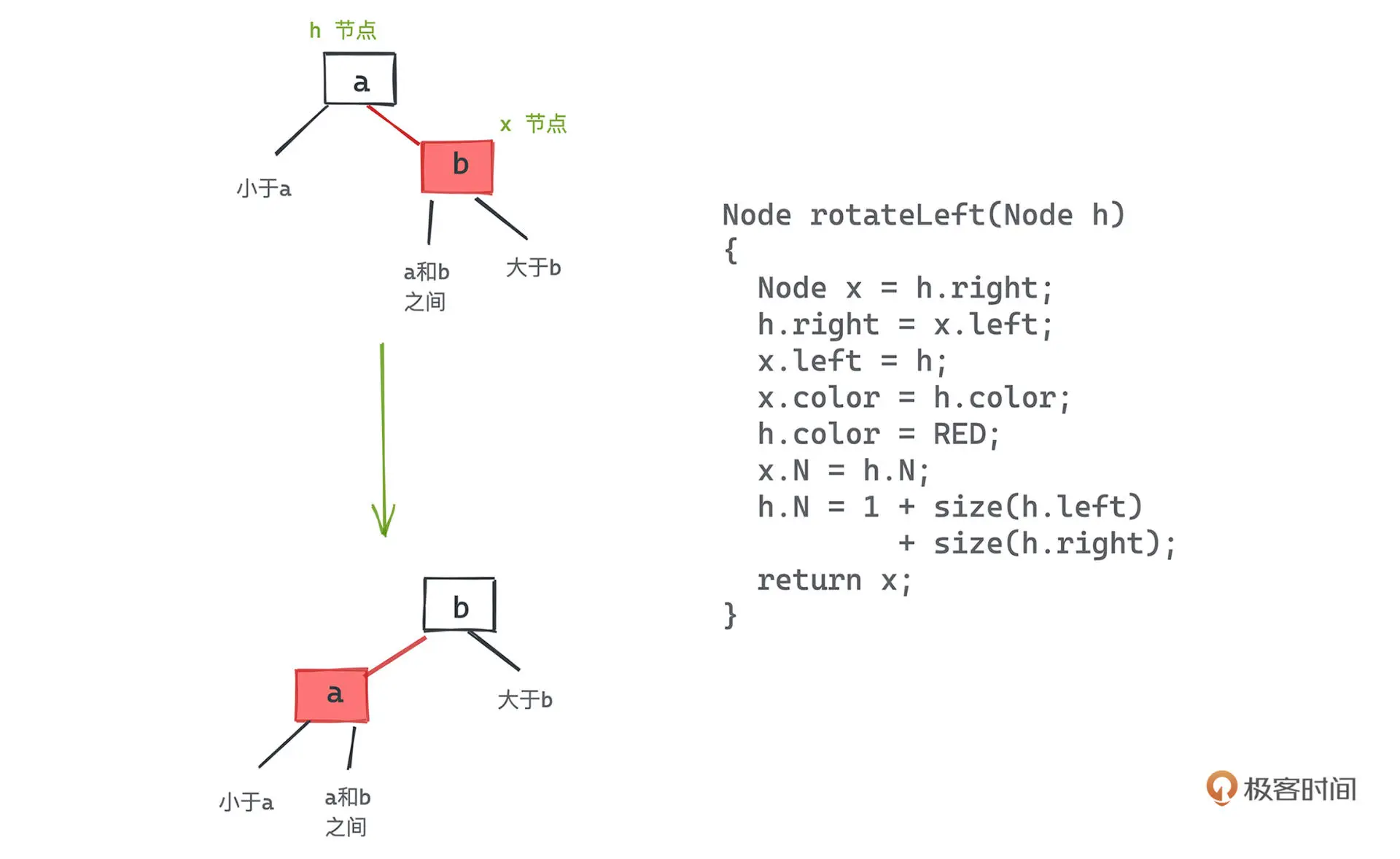
反色
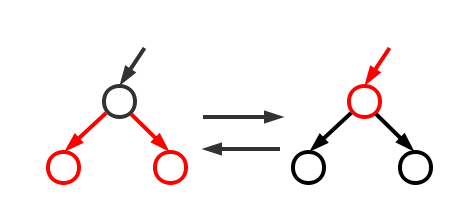
插入
新插入的节点均设为红色
黑节点插入
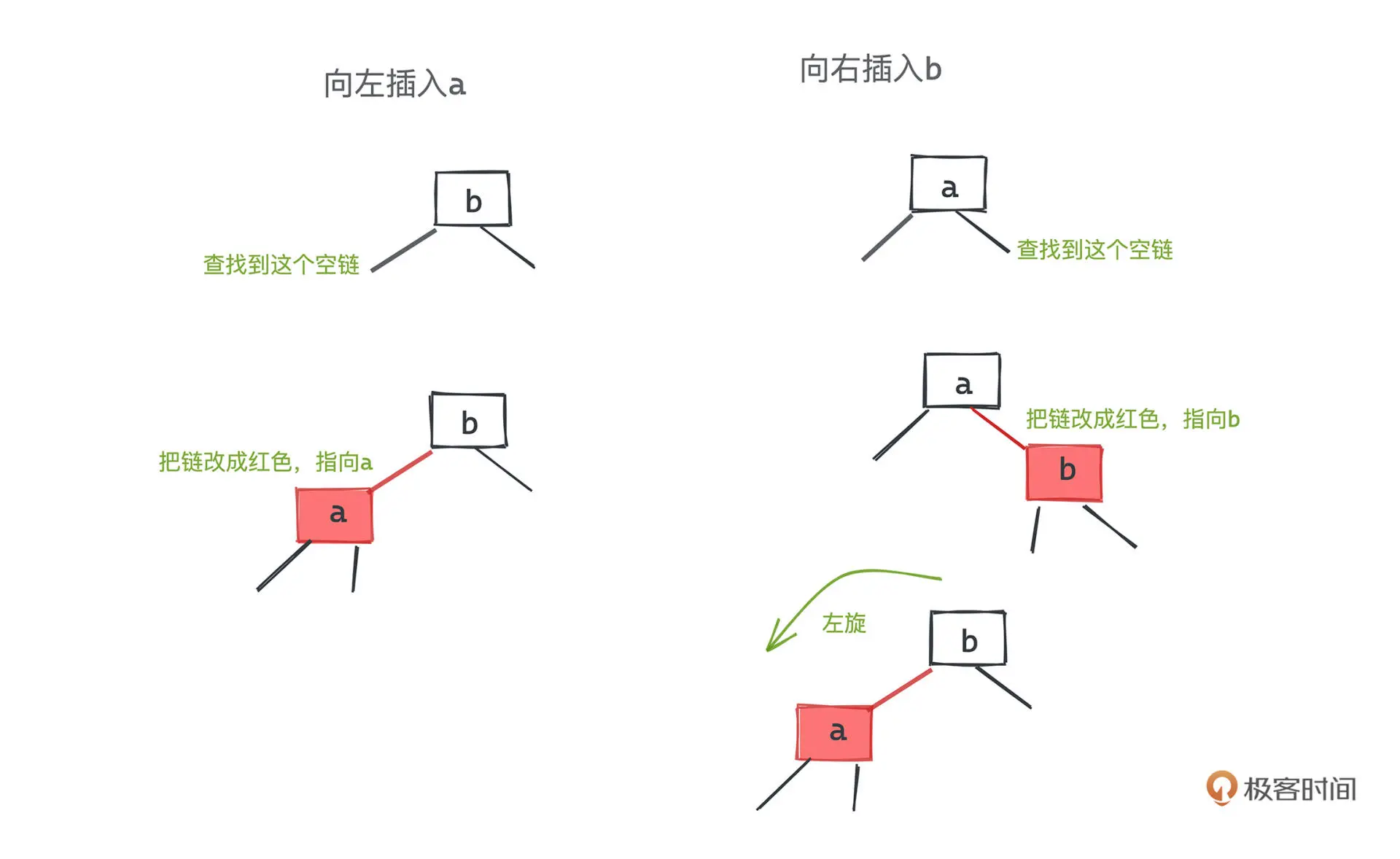
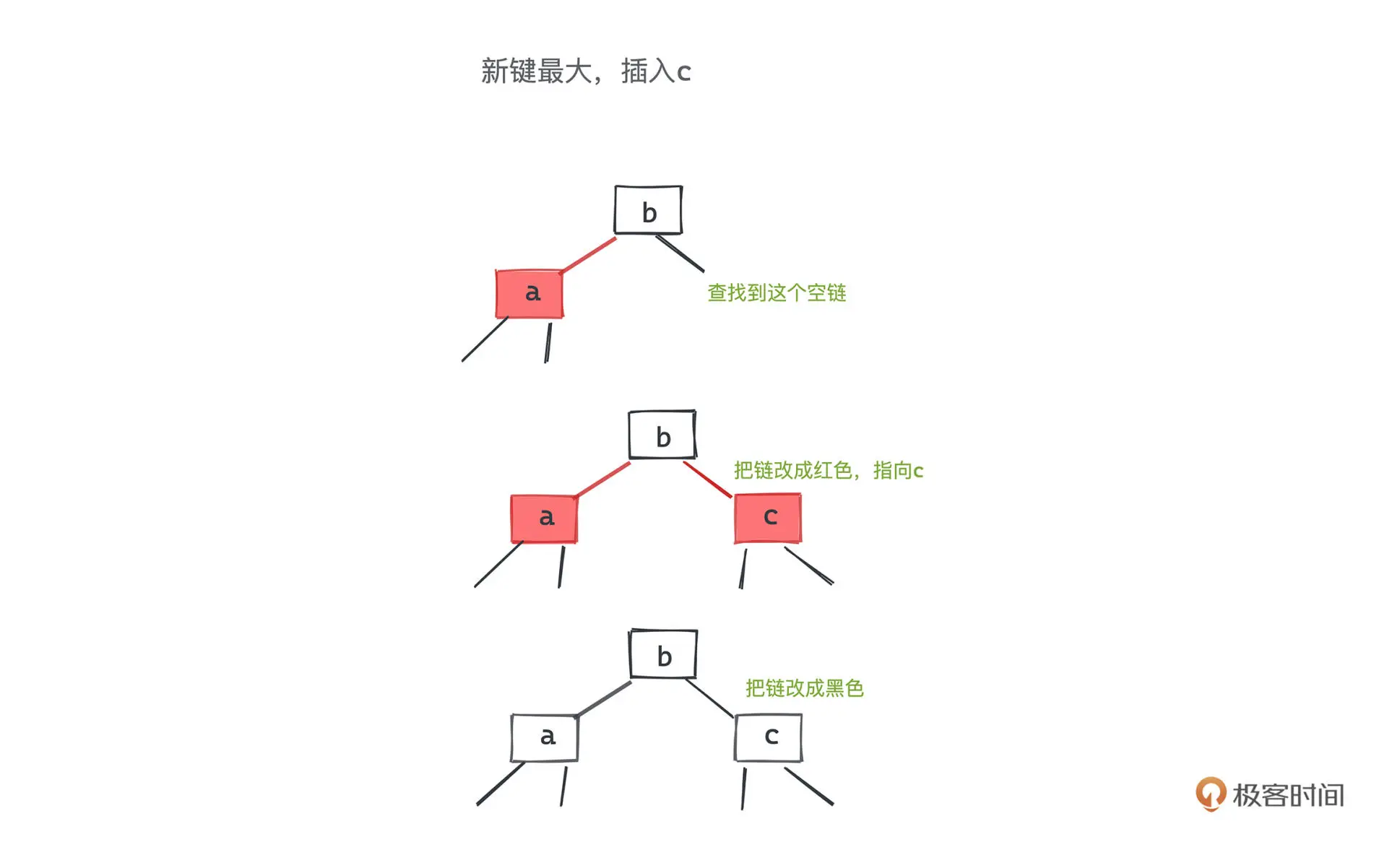
红节点插入
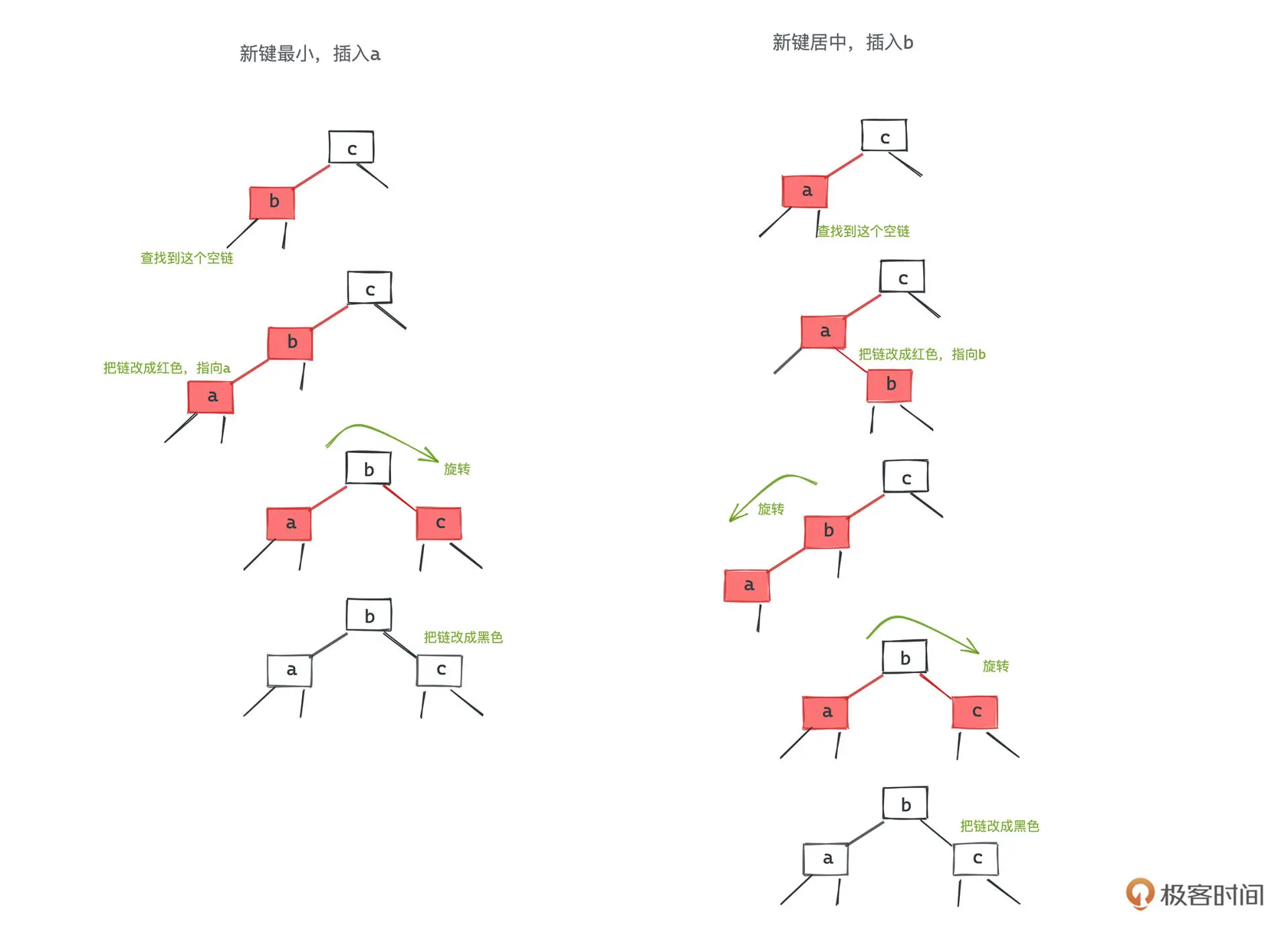
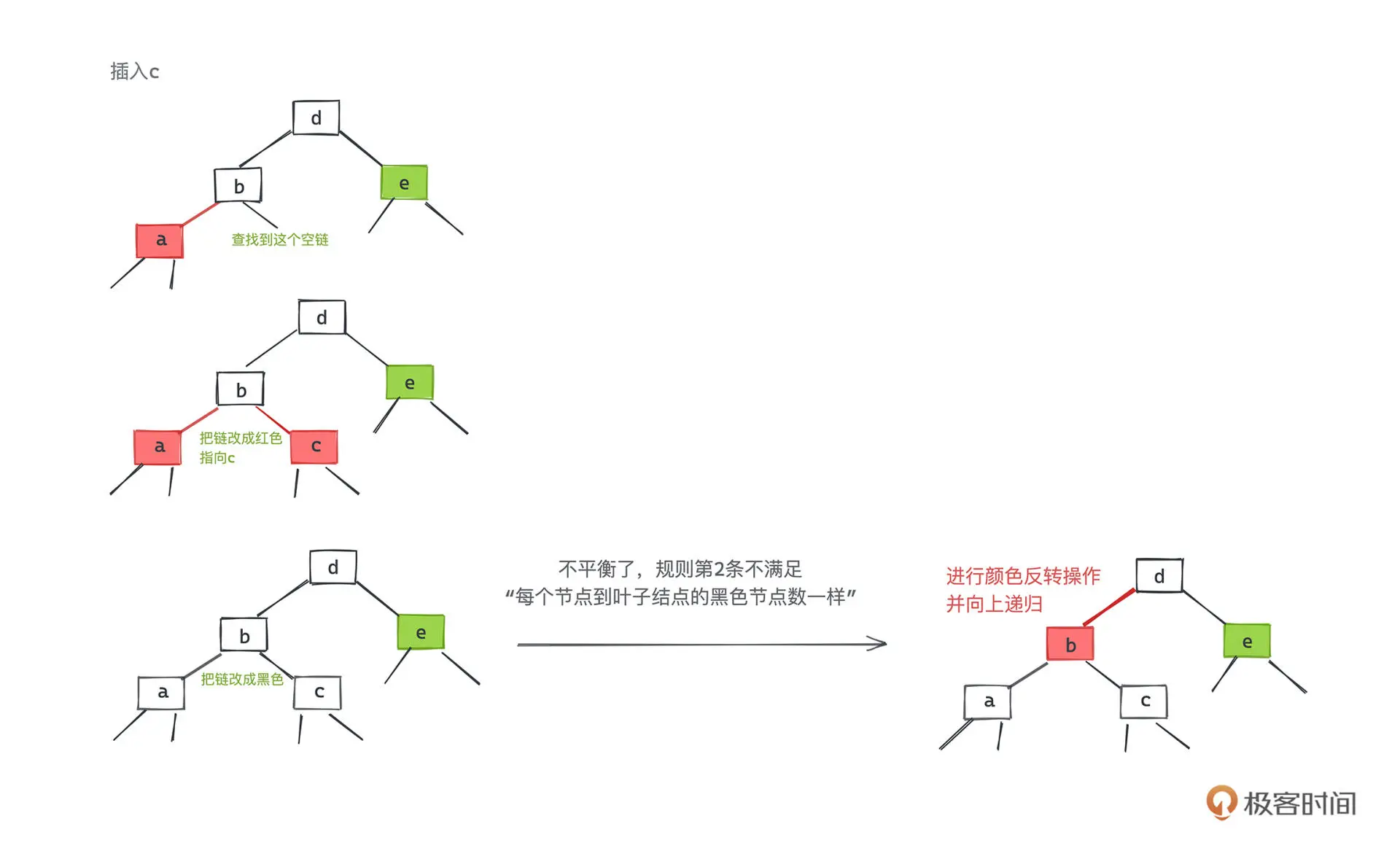
删除
散列表
根据键(Key)而直接访问在内存存储位置的数据结构,也就是说,它通过计算一个关于键值的函数,将所需查询的数据映射到表中一个位置来访问记录,这加快了查找速度
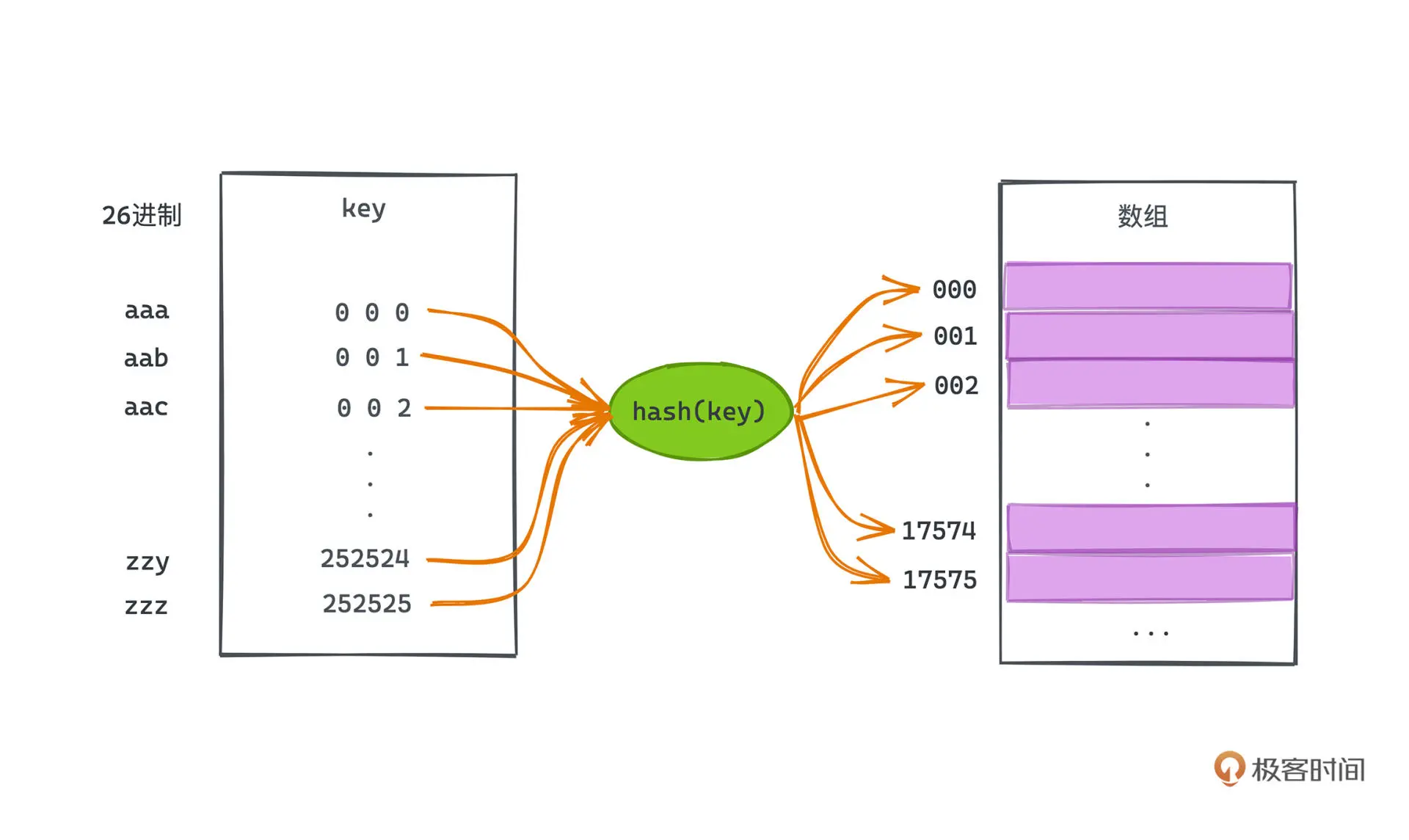
散列函数
这个过程会将键转化为数组的索引
把任意长度的输入(又叫做预映射pre-image)通过散列算法变换成固定长度的输出,该输出就是散列值
设计散列函数
- 要保证散列函数输出的数值是一个非负整数,因为这个整数将是散列表底层数组的下标
- 在使用有限数组空间的前提下,导致的哈希冲突尽量少
- 不宜过于复杂
散列冲突
当不同的输入得到相同的hash值时,称为散列冲突
解决:拉链法
当发生碰撞的时候,拉链法是将碰撞的元素串成一个链表
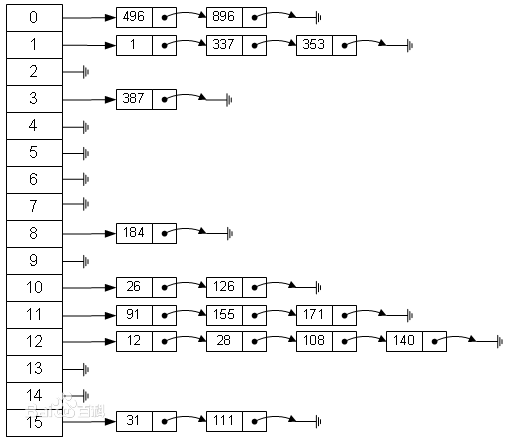
解决:线性探测
当发生碰撞的时候,直接检查散列表中的下N个位置(N可正可负)
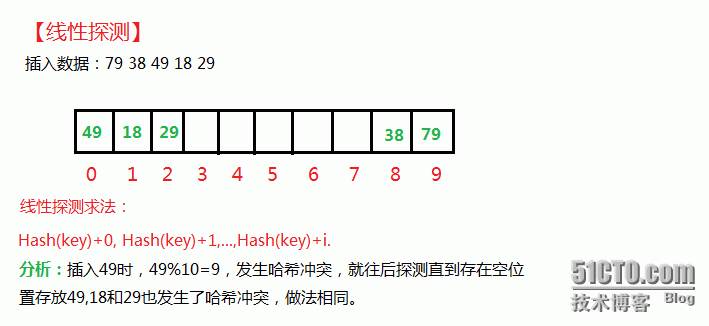
- 在查找的时候,如插入一样一直进行线性探测,直至碰到一个键为空的槽
删除
删除的时候,不能简单地将槽置为空,需要将与该键同散列值的键都往前移动,填补因为该键被删除而造成的空缺
调整大小
当数组大小发生改变,不能直接位置一对一迁移,而是需要对先前的每个元素,重新计算散列(rehash),重新放入槽
java中的实现
JDK8后,HashMap当冲突列表超过8个之后,会使用红黑树
时间轮
round时间轮
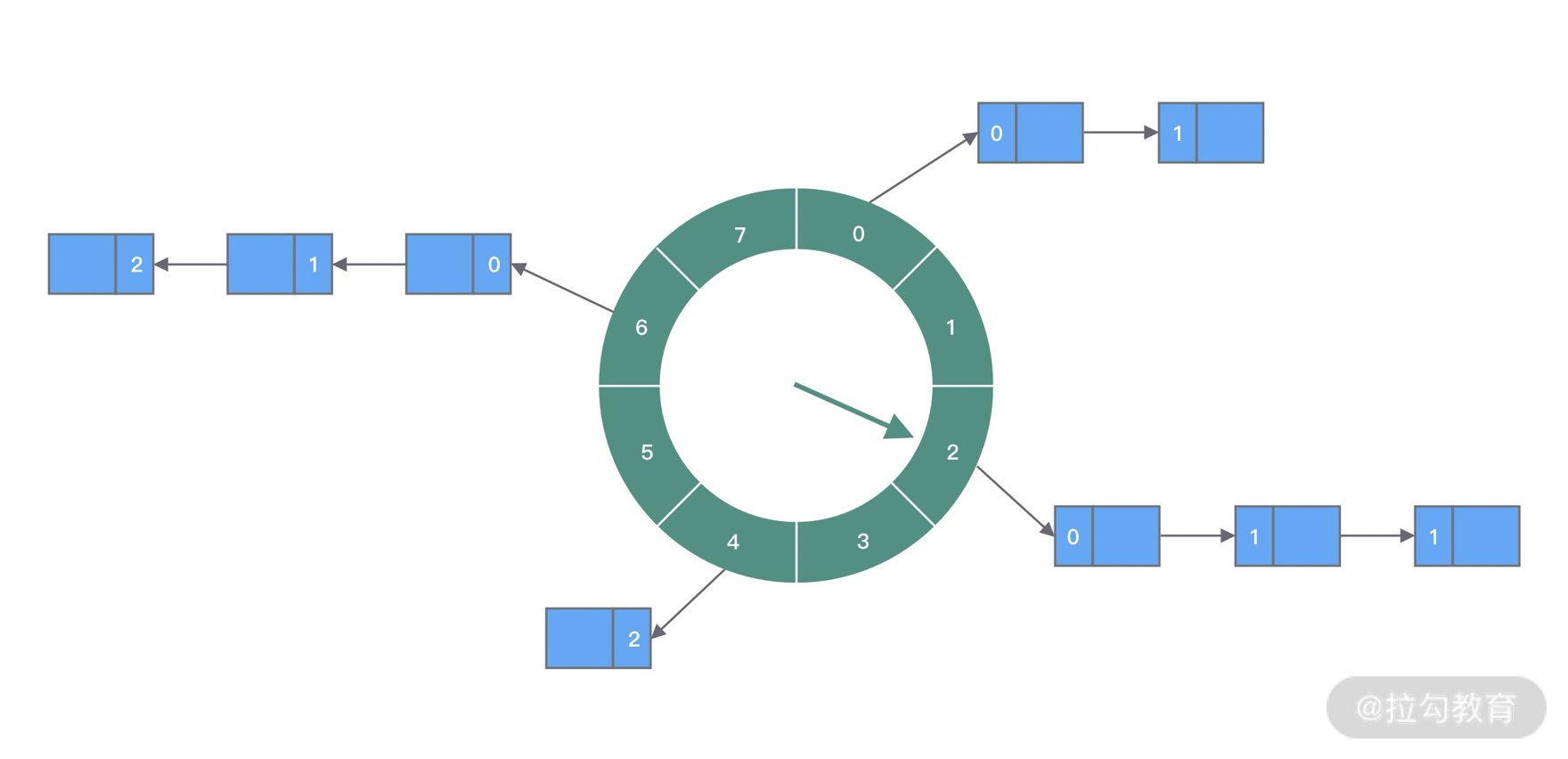
时间轮被划分为 8 个 slot,每个 slot 代表 1s,当前时针指向 2。假如现在需要调度一个 3s 后执行的任务,应该加入 2+3=5 的 slot 中;如果需要调度一个 12s 以后的任务,需要等待时针完整走完一圈 round 零 4 个 slot,需要放入第 (2+12)%8=6 个 slot
怎么区分每个任务是否需要立即执行,还是需要等待下一圈 round,甚至更久时间之后执行呢?所以我们需要把 round 信息保存在任务中。例如图中第 6 个 slot 的链表中包含 3 个任务,第一个任务 round=0,需要立即执行;第二个任务 round=1,需要等待 18=8s 后执行;第三个任务 round=2,需要等待 28=8s 后执行。所以当时针转动到对应 slot 时,只执行 round=0 的任务
分层时间轮
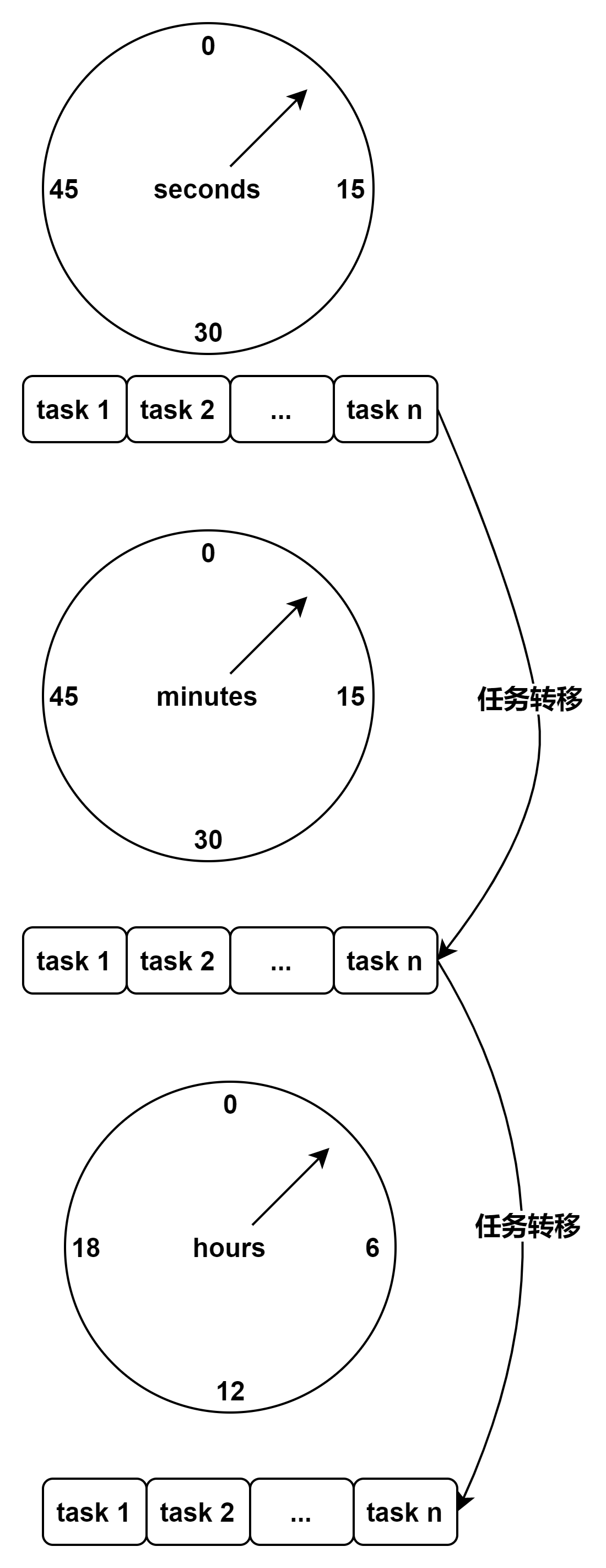
当上层的时间轮转完一圈时,下层的定时器就要增加一个刻度
假设我们的任务需要在每天的 7:30:20 秒执行一次。任务首先添加于小时级别时钟轮的第 7 号刻度上,当其轮询线程访问到第 7 号刻度时,就将此任务转移到分钟级别时钟轮的第 30 号刻度上。当分钟级别的时钟轮线程访问到第 30 号刻度,就将此任务转移到秒级别时钟轮的第 20 号刻度上。当秒级别时钟轮线程访问到第 20 号刻度时,最终会将任务交给异步线程负责执行