数据挖掘
基本流程
商业理解是数据挖掘项目成功的关键之一,因为这有助于确保项目从一开始就是针对商业目标而设计的。
数据理解和数据准备是数据挖掘的重要前提,因为数据质量对于最终的模型效果至关重要。
模型建立和模型评估是数据挖掘的核心步骤,这是构建和测试模型的关键阶段。
上线发布是数据挖掘项目的最终目标,因为这意味着模型已经被应用到商业实践中,并且提供了有价值的商业洞察。
监控和维护是确保数据挖掘结果持续有效的关键步骤,因为数据和商业需求都在不断变化,需要定期评估和更新模型
数据挖掘背后的数学原理:
- 概率论与数理统计:提供了数据建模和推断的理论基础
- 线性代数:特别是矩阵与向量
- 图论:来描述数据的结构关系
- 最优化方法:解决优化问题的工具
数据挖掘的任务
- 分类(Classification):分类是将数据划分到不同的类别或标签中的任务。它通常用于有标记的数据,即每个数据都有一个预先定义好的标签。分类的目标是构建一个模型,该模型可以根据数据中的特征将未标记的数据分配到正确的类别中。
- 聚类(Clustering):聚类是将数据划分为具有相似特征的组或簇的任务。聚类是一种无监督学习,即数据没有预先定义的标签或类别。聚类的目标是在数据中发现内在的结构或模式,并将数据分组为具有相似特征的组。
- 预测(Prediction):预测是使用历史数据中的模式和关系来预测未来数据的任务。预测通常用于连续型数据,即数值型数据,而不是分类数据。预测的目标是构建一个模型,该模型可以使用历史数据来预测未来数据。
- 关联分析(Association Analysis):关联分析是发现数据之间关系的任务。它通常用于交易数据,例如购物篮数据。关联分析的目标是发现数据中的频繁项集和关联规则,这些规则可以揭示数据之间的关系和模式。
关联规则挖掘
关联规则挖掘可以从数据集中发现项与项(item 与item)之间的关系
支持度
指一组频繁模式的出现概率,表示项集{X,Y}在总项集里出现的概率。表示A和B同时在总数I 中发生的概率
$$ Support(X,Y) = P(XY) = \frac{number(X,Y)}{number(总样本)} $$
置信度
衡量频繁模式内部的关联关系,体现了一个数据出现后,另一个数据出现的概率
$$ Confidence(X ⇐ Y) = P(X|Y) = \frac{P(X|Y)}{P(Y)} $$
提升度
表示含有X的条件下,同时含有Y的概率,与只看Y发生的概率之比。提升度反映了关联规则中的X与Y的相关性,提升度>1且越高表明正相关性越高,提升度<1且越低表明负相关性越高,提升度=1表明没有相关性,即相互独立
$$ Lift(X → Y) = \frac{P(Y|X)}{P(Y)} $$
Apriori 算法
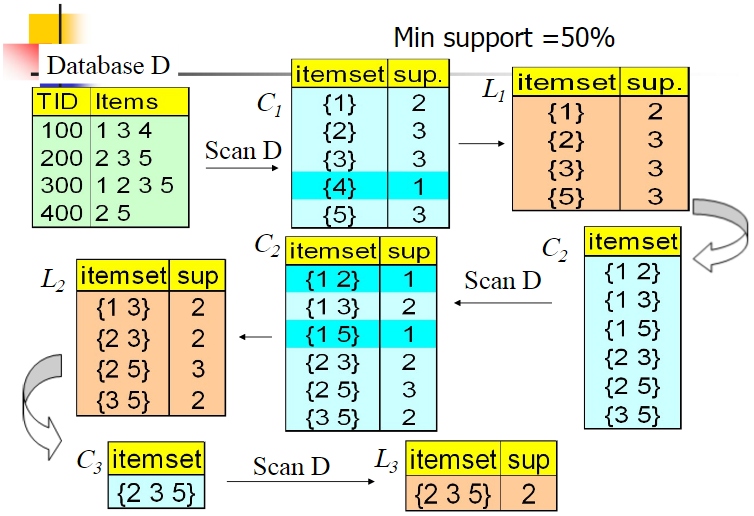
如果 123 是频繁组合,则 12、13、23 也是频繁组合;若 12 是非频繁组合,则 123 也是非频繁组合
FP-Growth 算法
创建了一棵 FP 树来存储频繁项集。在创建前对不满足最小支持度的项进行删除,减少了存储空间,整个生成过程只遍历数据集 2 次
聚类
分级聚类
不断将最为相似的群组两两合并
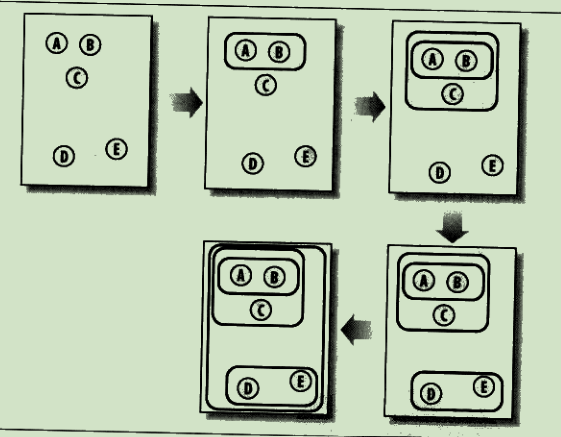
使用树状图来可视化聚类结果,通过路径长度来体现各元素的相似度:
stateDiagram-v2
direction LR
cluster --> cluster1
cluster1 --> cluster3
cluster3 --> A
cluster3 --> B
cluster1 --> C
cluster --> cluster2
cluster2 --> D
cluster2 --> E
K-均值聚类
- 随机确定k个中心位置
- 将各个数据项分配个最近的中心点
- 将中心点移动到各个节点的平均位置
- 重复2-3 直到不再变化
如果某个点比较倒霉,初始被分配到的地方找不到与其最近的点,那一般就会把这个聚类去掉,变成 K - 1 个聚类
所以,代价函数是
$$ J =\frac{1}{m}\sum_{i=1}^{m}|x^{(i)}-\mu_{c^{(i)}}|^{2} $$
如果代价函数值增加了,一定是实现出了问题
选择初始点:
- K要小于训练数据数量
- 随机从训练数据中挑选 K 个点作为初始点
- 这种随机初始化有可能找到的是局部最优解,所以需要多轮随机选择,选择代价函数最小的初始点
选择K:
- 一种办法是尝试不同的K,使用代价函数较小,K也合适的,这会导致算法偏向于更大的K
- 另外一种选择K的办法是K应该是要跟解决的问题相关,要根据业务来决定
EM聚类
stateDiagram-v2
初始化参数 --> 观察预期: Exception
观察预期 --> 重新估计参数: Maximization
重新估计参数 --> 初始化参数
EM 算法相当于一个框架,你可以采用不同的模型来进行聚类,比如 GMM(高斯混合模型),或者 HMM(隐马尔科夫模型)来进行聚类
AdaBoost
通过训练多个弱分类器,将它们组合成一个强分类器
假设弱分类器为 Gi(x),它在强分类器中的权重 αi,那么就可以得出强分类器 f(x):
$$ f(x)=\sum_{i=1}^n\alpha_iG_i(x) $$
如果弱分类器的分类效果好,那么权重应该比较大,如果弱分类器的分类效果一般,权重应该降低
优化
- 随机优化:对拥有大量题解的一个问题,选取一个可优化的题解进行优化
蒙特卡洛算法和拉斯维加斯算法
- 两类算法的统称,利用随机的方法来简化整体的算法过程
蒙特卡罗算法原理:每次计算都尽量尝试找更好的结果路径,但不保证是最好的结果路径。用这样寻找结果的方法,无论何时都会有结果出来,而且给的时间越多、尝试越多,最终会越近似最优解
拉斯维加斯算法原理:就是每次计算都尝试找到最好的答案,但不保证这次计算就能找到最好的答案,尝试次数越多,越有机会找到最优解
成本函数
用一个值代表方案的好坏程度 值越大代表方案越差,对于一个问题,会有多种变量,则需要对这些变量进行归一化计算,从而确定哪些变量更重要
若果可能,让最优解的成本函数为0,这样子当找到最优解后就可以停止后续的查找
随机搜索
生成一定范围内的随机题解,代入成本函数,也许可以得到一个可以接受的题解
爬山法
随机选取一个题解,在这个题解临近的解题空间内寻找成本更低的题解
这种方式问题是得到题解的可能只是局部最优而非全局最优
模拟退火算法
随机选取一个题解,然后也会跟爬山法一样尝试寻找成本更低的解
区别在于如果发现新的题解比老的题解花费的成本更高,这个题解可能也会被接收(随机),但随着迭代次数不断增加(温度下降),这种花费成本更高的题解被接受的概率会越来越小
遗传算法
随机选取一组题解,对这些题解的成本函数进行排序
选取成本函数最小的一部分顶端题解,称之为精英选拔,创建新种群,新种群的其他题解都是根据这些精英演变而来的
演变的方式有两种:
- 变异:对题解的某一个变量做一个微小的调整
- 配对:调两个题解按某种方式进行交叉结合
分类
- 纯度:数据集中的样本全部属于同一类别,即数据集完全“纯”的程度
- 熵:集合的混乱程度越高,熵越高,熵为0时,代表集合绝对有序,熵的计算: $H(p_{1})=-p_1log_2(p_1)-(1-p_1)log_2(1-p_1)$,$p_1$代表某一类在集合中的概率
决策树
需要对结构化的数据进行预测,在结果为某种分类时,适合使用。决策树尝试得到训练数据的多棵决策树,从中选择一个效果最好的
stateDiagram-v2
根条件 --> 条件1
根条件 --> 条件2
条件1 --> 条件3
条件1 --> 条件4
条件3 --> 结果1
条件4 --> 结果2
条件2 --> 结果1
- 根条件的选择:选择能将左右分支两个集合的熵划分的最小的条件
- 何时停止划分
- 节点下的集合都属于同一个分类
- 树已经达到了最大深度,继续划分只会变得过拟合
- 划分带来的纯度提升小于设定阈值
- 节点下集合项小于设定阈值
使用信息增益衡量每次划分减少了多少熵,结果越大代表减少的熵越多:
$$ H(p_1^{root}-\left(w^{left}H\left(p_1^{left}\right)+w^{right}H\left(p_1^{right}\right)\right) $$
对于取指不止两个的特征,可以采取 one-hot 编码,如果一个特征有 k 个取指,那就可以把它转换成 k 个只能取0 1 的特征
对于拥有连续值的特征,则需要多次尝试不同的取值,使得以该值划分的两类集合获得的信息增益最高
剪枝
训练出来的决策树可能会对训练数据过拟合,所以需要在合适的情况下停止拆分决策树的子节点
预剪枝:在构造的过程中对节点进行评估,如果对某个节点进行划分,在验证集中不能带来准确性的提升,就不对其进行拆分
后剪枝:构造完决策树之后,逐层向上对每个节点进行评估。如果剪掉这个节点子树,与保留该节点子树在分类准确性上差别不大,或者剪掉该节点子树,能在验证集中带来准确性的提升,那么就可以把该节点子树进行剪枝。方法是:用这个节点子树的叶子节点来替代该节点,类标记为这个节点子树中最频繁的那个类
ID3算法
计算的是信息增益,就是划分可以带来纯度的提高,倾向于选择取值比较多的属性,但这个属性可能对于分类并没有太大作用
C4.5算法
- 采用信息增益率的方式来选择属性。信息增益率 = 信息增益 / 属性熵
- 悲观剪枝:递归估算每个内部节点的分类错误率,比较剪枝前后这个节点的分类错误率来决定是否对其进行剪枝
- 对于连续属性的处理是通过将连续属性离散化来实现,选择具有最高信息增益的划分所对应的阈值
- 对于缺失值所在的样本,将其划分到各个子集中,并计算其对应的信息增益,最终选择信息增益最大的子集进行划分
CART算法
- Classification And Regression Tree,分类回归树
分类树处理离散数据,输出样本类别;回归树处理连续数据,输出回归预测
基尼系数是一种衡量纯度的方法:随机选取两个样本,其类别不一致的概率,这个概率越低则样本最稳定
CART 分类树算法中,基于基尼系数对特征属性进行二元分裂
CART 回归树算法中,根据样本的混乱程度,也就是样本的离散程度来评价“不纯度”
剪枝:采用的是代价复杂度剪枝方法
随机森林
一个包含多个决策树的分类器,每一个子分类器都是一棵 CART 分类回归树
为了随机构造多棵树,需要使用采样替换技术:每次随机抽取一条训练数据记录,放回,重新抽取并重复这个过程,这样可以生成多份随机的训练,并使用这些随机的训练数据去生成多颗决策树
做分类的时候,输出结果是每个子分类器的分类结果中最多的那个,做回归的时候,输出结果是每棵 CART 树的回归结果的平均值
XGBoost
时间序列预测
- Auto Regressive:自回归模型。这个算法的思想比较简单,它认为过去若干时刻的点通过线性组合,再加上白噪声就可以预测未来某个时刻的点
- Moving Average:滑动平均模型。它与 AR 模型大同小异,AR 模型是历史时序值的线性组合,MA 是通过历史白噪声进行线性组合来影响当前时刻点
- Auto Regressive Moving Average:自回归滑动平均模型,也就是 AR 模型和 MA 模型的混合
- Auto Regressive Integrated Moving Average:相比于 ARMA,ARIMA 多了一个差分的过程,作用是对不平稳数据进行差分平稳,在差分平稳后再进行建模
回归树
每一片叶子都输出一个预测值。预测值一般是该片叶子所含训练集元素输出的均值
回归树中每个节点选择那个特征,都遵循划分使得一个节点下所有值的方差最小的原则,这点跟使用信息增益来分裂节点原理一样
KNN
找出k个与当前元素相似的元素,对这些元素求均值,从而做出对当前元素的预测
过多或过少的k都会导致结果不准
如果 K 值比较小,就相当于未分类物体与它的邻居非常接近才行。这样产生的一个问题就是,如果邻居点是个噪声点,那么未分类物体的分类也会产生误差,这样 KNN 分类就会产生过拟合。
如果 K 值比较大,相当于距离过远的点也会对未知物体的分类产生影响,虽然这种情况的好处是鲁棒性强,但是不足也很明显,会产生欠拟合情况,也就是没有把未分类物体真正分类出来。一般采用交叉验证的方式选取 K 值
近邻权重
将相似度(距离)转为权重
- 反函数:距离的导数
- 减法函数:使用一个常量减去距离,如果为正数,则权重就是为该正数,否则权重为0
- 高斯函数:在距离为0时权重为1,随着距离增加无限接近0
加权K-最近邻
- 每个元素的值需要乘以权重
线性分类
- 构造分类中所有数据的平均值为中心点,新的数据根据距离离中心点的距离判断是哪类
核技法
支持向量机SVM
常见的一种分类方法,在机器学习中,SVM 是有监督的学习模型
SVM 就是帮我们找到一个超平面,这个超平面能将不同的样本划分开,同时使得样本集中的点到这个分类超平面的最小距离(即分类间隔)最大化,SVM 就是求解最大分类间隔的过程
硬间隔指的就是完全分类准确,不能存在分类错误的情况。软间隔,就是允许一定量的样本分类错误
非线性SVM:有些数据样本没法通过线性函数划分,就引入核函数将样本从原始空间映射到一个更高维的特质空间中,使得样本在新的空间中线性可分
多分类问题:SVM 本身是一个二值分类器,最初是为二分类问题设计的,可以将多个二分类器组合起来形成一个多分类器:
- 一对多:把其中的一类作为分类 1,其他类统一归为分类 2
- 一对一:在任意两类样本之间构造一个 SVM,每一个分类器都会有一个分类结果,得票多者胜
费舍尔方法
模型评估
离线评估
Holdout 检验:将原始的样本集合随机划分为训练集和测试集两部分,评估的结果有一定随机性
交叉校验:为了消除 Holdout 检验的随机性,将全部样本划分成 k 个大小相等的样本子集,然后依次遍历这 k 个子集,每次把当前遍历到的子集作为验证集,其余所有的子集作为训练集,这样依次进行 k 次模型的训练和评估,再将所有 k 次评估指标的平均值作为最终的评估指标
自助法:对于总数为 n 的样本集合,先进行 n 次有放回地随机抽样,得到大小为 n 的训练集。在 n 次采样过程中,有的样本会被重复采样,有的样本没有被抽出过,再将这些没有被抽出的样本作为验证集进行模型验证
时间切割:将时间序列数据分为训练集和测试集,在某一个时间点之前的数据用作训练集,之后的数据用作验证集,防止模型在训练和评估过程中引入未来信息
离线 Replay:根据数据生成时间对测试样本进行排序,并根据模型的更新时间点,逐步更新模型并评估模型在更新前后的性能,以更准确地反映模型在生产环境中的表现
评估指标
- 正样本:即属于某一类的样本
- 负样本:即不属于某一类的样本
| 对比项 | 正类 | 负类 |
|---|---|---|
| 被检索 | True Positive | False Positive |
| 未检索 | False Negative | True Negative |
- 准确率(Accuracy):指分类正确的样本占总样本个数的比例 $(TP + TN) / ALL$
- 查准率(Precision):被正确检索的样本数 与 被检索到样本总数之比 $TP / (TP + FP)$
- 查全率(Recall):被正确检索的样本数 与 应当被检索到的样本数之比 $TP / (TP + FN)$
宁愿漏掉,不可错杀:Precision 将是一个被侧重关心的指标。宁愿错杀,不可漏掉:Recall 将是一个被侧重关心的指标。当两个数字都很高时,表示模型有很好的效果
F-Score,用来综合考虑 Precision 与 Recall,$\beta$是用来调整 Precision 与 Recall 二者的权重,这个分数越高代表 Precision 与 Recall 更平衡:
$$ FS=\left(1+\beta^2\right)\cdot\frac{Precision\cdot Recall}{\beta^2\cdot(Precision+Recall)} $$
对数损失:
$$ \begin{aligned}-\frac{1}{N}\sum_{i=1}^{N}\left(y_i\log P_1+(1-y_i)\log\left(1-P_i\right)\right)\end{aligned} $$
(二分类对数损失函数)
yi 是输入实例 xi 的真实类别, pi 是预测输入实例 xi 是正样本的概率,N 是样本总数
(多分类对数损失函数)
$$ \text{Multi-LogLoss }=-\frac1n\sum_{i=1}^n\sum_{j=1}^my_{i,j}\log{(p_{i,j})} $$
均方根误差:用来评估预测连续值的模型的效果
$$ \mathrm{RMSE}=\sqrt{\frac{\sum_{i=1}^n\left(y_i-\hat{y}_l\right)^2}n} $$
yi 是第 i 个样本点的真实值,y^l 是第 i 个样本点的预测值,n 是样本点的个数。那么均方根误差越小,就证明这个回归模型预测越精确
P-R曲线:横轴是召回率,纵轴是精确率,可以用来对比不同模型在固定召回率或精确率的情况,另外一个指标怎样
ROC曲线:横坐标是 False Positive Rate(FPR,假阳性率),纵坐标是 True Positive Rate (TPR,真阳性率)
平均精度均值: