数字逻辑电路基础
数制
- 十进制
(1) 计数符号: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
(2) 进位规则: 逢十进一.
- 二进制
(1) 计数符号: 0, 1 。
(2) 进位规则: 逢二进一
- 十六进制
(1)计数符号: 0,1,......,9,A,B,C,D,E,F
(2)进位规则: 逢十六进一。
- 八进制
(1)计数符号: 0,1,......,6,7。
(2)进位规则: 逢八进一。
二进制转十进制
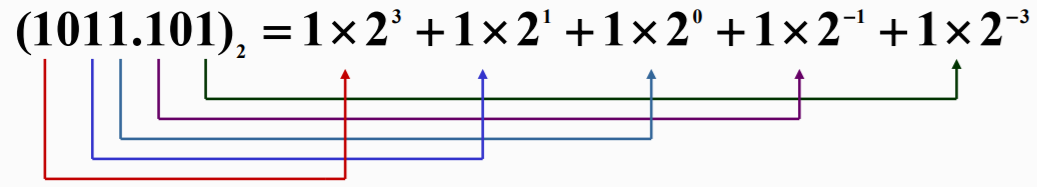
十进制转二进制
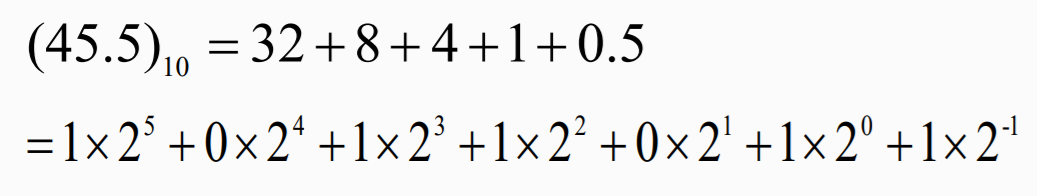
二进制算术元算
二进制加法规则
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 产生进位1
二进制减法规则
0 - 0 = 0
1 - 1 = 0
1 - 0 = 1
10 - 1 = 1 产生借位1
二进制乘法规则
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
二进制除法
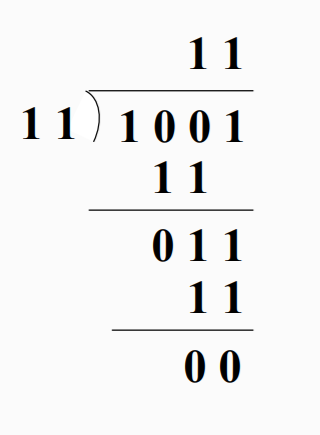
补码
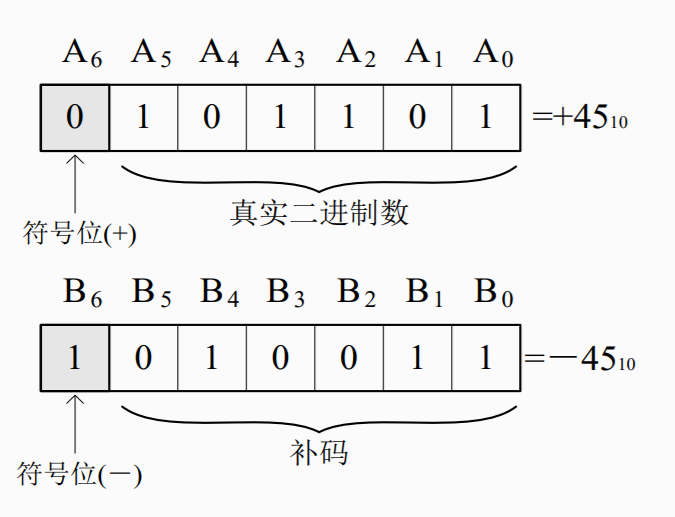
加法
当两个正数或者两个负数相加时,如果相加结果的符号位与两个相加数的符号位不同,则产生了溢出
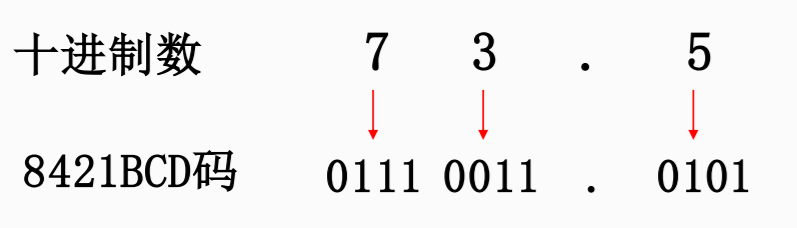
二-十进制码(BCD码)
用四位二进制码来表示一位十进制数字
格雷码(Gray码)
相邻两个代码之间仅有一位不同,其余各位均相同

应用:轴角编码器
ASCII码
美国信息交换标准代码:ASCII
扩展ASCII码(0-255)
奇偶校验码
在原码组的基础上增加一个码位使码组中含1的个数为奇数(称为奇校验)或偶数(称为偶校验)。
逻辑代数
在逻辑代数中,变量常用字母A,B,C, ......,X,Y,Z,a, b, c ,......x,y,z 等表示,变量的取值只能是"0"或"1",这种变量称为逻辑变量
逻辑代数中只有三种基本逻辑运算,即"与"、"或"、"非"
- 与逻辑运算
定义:只有决定一事件的全部条件都具备时,这件事才成立;如果有一个或一个以上条件不具备,则这件事就不成立。这样的因果关系称为"与"逻辑关系
- 或逻辑运算
定义:在决定一事件的各种条件中,只要有一个或一个以上条件具备时,这件事就成立;只有所有的条件都不具备时,这件事才不成立。这样的因果关系称为"或"逻辑关系
- 非逻辑运算
定义:假定事件F成立与否同条件A的具备与否有关,若A具备,则F不成立;若A不具备,则F成立。F和A之间的这种因果关系称为"非"逻辑关系
复合逻辑运算
- 与非逻辑
!(a&&b)
- 或非逻辑
!(a||b)
- 与或非逻辑
!((a&&b)||(c&&d))
- 异或逻辑
(!a&&b) || (a&&!b)
- 同或逻辑
!a&&!b || a&&b
逻辑电平
- 正逻辑
高电平VH表示逻辑"1",低电平VL表示逻辑"0"
- 负逻辑
高电平VH表示逻辑"0",低电平VL表示逻辑"1"
VH和VL的具体值,由所使用的集成电路品种以及所加电源电压而定
基本定律
两个函数的真值表相等,则这两个函数一定相等

三条规则
- 代入规则
任何一个含有变量x的等式,如果将所有出现x的位置,都用一个逻辑函数式F代替,则等式仍然成立
- 反演规则
对于任意一个函数表达式Y,如果把Y中所有的“与”换成“或”,“或”换成“与”;“0”换成“1”,“1”换成“0”;原变量换成反变量,反变量换成原变量,即得到一个新的函数表达式Y非,称Y非为原函数Y的反函数
- 对偶规则
对于任何一个逻辑表达式F,如果将式中所有的“·”换成“+”,“+”换成“·”,“0”换成“1”,“1”换成“0”,而变量保持不变就得到表达式F',这个表达式F'称为F的对偶式,这一变换方式称为对偶规则
常用公式
- 消去律

- 吸收律1

- 吸收律2
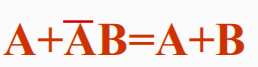
- 包含律
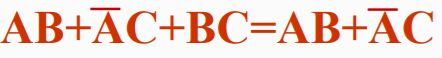
逻辑表达式
- “与或”式
指一个函数表达式中包含若干个“与”项,这些“与”项的“或”表示这个函数
F(A,B,C,D)=A+BC+ABCD
- “或与”式
指一个函数表达式中包含若干个“或”项,这些“或”项的“与”表示这个函数
F(A,B,C,D)=(A+C+D)(B+D)(A+B+D)
最小项与最大项
如果一个具有n个变量的函数的“与项”包含全部n个变量,每个变量以原变量或反变量形式作为因子出现一次,而且仅出现一次,则这种“与项”被称为最小项
如果一个具有n个变量的函数的“或项”包含全部 n个变量,每个变量以原变量或反变量形式作为因子出现一次,而且仅出现一次,则这种“或项”被称为最大项。
- 标准与或式
如果一个逻辑表达式为与或式,而且其中每个与项都是最小项,则称该逻辑表达式为标准与或式
- 标准或与式
如果一个逻辑表达式为或与式,而且其中每个或项都是最大项,则称该逻辑表达式为标准或与式
真值表
- 逐个代入
- 求最小项取值为1的组合
- 根据函数表达式F的含义,直接填表
化简
- 节省元器件,降低电路实现成本
- 提高电路工作可靠性
化简的方式
- 公式法
- 卡诺图法
最简与或式的标准
- 所得与或表达式中,乘积项(与项)数目最少
- 每个乘积项中所含的变量数最少
卡诺图
卡诺图是一种包含一些小方块的几何图形,图中每个小方块称为一个单元,每个单元对应一个最小项。两个相邻的最小项在卡诺图中也必须是相邻的
不完全确定的逻辑函数
在某些实际数字电路中,逻辑函数的输出只和一部分最小项有确定对应关系,而和余下的最小项无关。把这些最小项称为无关项
包含无关项的逻辑函数称为不完全确定的逻辑函数