机器学习

频率视角下的机器学习：认为模型待估计的参数是固定不变的常量，用来估计参数的数据是随机的变量，需要我们通过某种手段（比如极大似然法）利用数据找到最优参数，损失函数（loss function）直接定义了模型性能的度量方式，其数学期望被称为风险（risk），风险最小化就是参数估计的依据和准则，用训练数据的经验分布替换掉原始表达式中数据的真实分布，借此找到最优参数

贝叶斯视角下的机器学习：将待估计的参数视为随机变量，用来估计的数据反过来是确定的常数，结合参数自身的分布特性，找到最可能产生观测数据的那个参数的过程，贝叶斯学习的输出是关于参数的概率分布

可被机器学习解决的问题：

1. 解决的问题会包含某些显式或者隐式的模式
2. 无法通过数值计算解决
3. 要有大量的可用数据

监督学习适用于预测任务，无监督学习适用于描述任务

• 批量学习：一口气对整个数据集进行建模与学习，并得到最佳假设
• 在线学习：算法根据数据的不断馈入而动态地更新
• 主动学习：有选择地询问无标签数据的标签来实现迭代式的学习

计算学习理论：关于通过”计算“来进行学习的理论，即关于机器学习的理论基础 目的：分析学习任务的困难本质，为学习算法提供理论保证，指导算法设计

监督学习

利用样本和期望输出来学习如何预测

• 回归问题：输出的结果是一个连续的值
• 分类问题：输出的结果是离散有限集合

无监督学习

在一组数据中寻找某种结构或模式

模型

• 参数模型：待求解的概率分布或者数量关系可以用一组有限且固定数目的参数完全刻画，最典型的是线性回归
• 非参数模型：认为存在一个未知的映射 f()˙​，输入通过这个映射转为输出，学习的对象也是这个映射

参数模型与非参数下模型的区别体现的是可解释性和精确性的区别

1. 模型拟合（model fitting）：利用训练数据集（training set）对模型的普通参数进行拟合
2. 模型选择（model selection）：利用验证数据集（validation set）对模型的超参数进行调整，筛选出性能最好的模型
3. 模型评价（model assessment）：利用测试数据集（test set）来估计筛选出的模型在未知数据上的真实性能

实验

实验设计的任务是观察一个或多个因子对实验结果的影响，因此包括算法类型、超参数、数据集等

• 一次一因子（控制变量法）：为所有因子都设定一个基线值，再在其他因子保持在基线水平的前提下令单个因子波动，观察它对学习性能的影响
• 全因子实验（full factorial experiment）：每个因子都有有限个离散的取值，实验则覆盖了所有因子所有取值的所有可能组合
• 连续实验（sequential experimentation）：首先执行全因子实验，但只给每个因子赋予较少的可能取值，确定哪些是对学习结果影响较大的活跃因子并保留下来，剩下的不活跃的因子就会被放弃
• 响应面方法（response surface methodology）：通过二次曲面的拟合寻找可变因子的最佳取值

特征工程

异常点会导致数据的有偏分布，如果异常点是由于采集出错，需要剔除这些异常点。如果异常点本身没有问题，除了剔除异常点之外，除了可以对所有特征值采取对数变化降低数值外，还能使用空间标识把异常点拉成正常

对于缺失的特征值，可以用 k 近邻方法和线性回归对特征的缺失值进行人为赋值

如果某个特征在绝大多数数据中的取值都是相同的，那这个特征就没有存在的意义，因为它体现不出对于不同分类结果的区分度，可以把这个特征去掉

• 特征选择：从现有特征集合中提取一部分作为特征
• 特征提取：对现有特征进行变化，组合得到新的特征，主成分分析将原始的共线性特征转化为新的正交特征，从而实现特征提取

向量化运算

可以充分利用GPU进行大规模并行

x = np.array([1,2,3])
y = np.array([3,2,1])
np.dot(x,y) # = for i in n: x[i] * y[i]

统计机器学习

线性回归模型

线性模型具有较强的可解释性

简单线性回归输出的因变量只与单个的输入自变量存在线性关系，而多元线性回归因变量由多个自变量共同决定

单变量线性回归模型：

$$ f(\mathbf{x})=w x + b = 模型(输入特征) = 输出结果 $$

多变量线性回归模型，使用向量表示多个特征及多个参数：

$$ f(\mathbf{\vec{x}})=\vec{w}\cdot \vec{x} + b = \sum_{i=0}^{n}w_i\cdot x_i + b $$

x 为自变量，w跟b被称为模型的参数，为了找出这两个参数，需要定义一个平方误差代价函数：

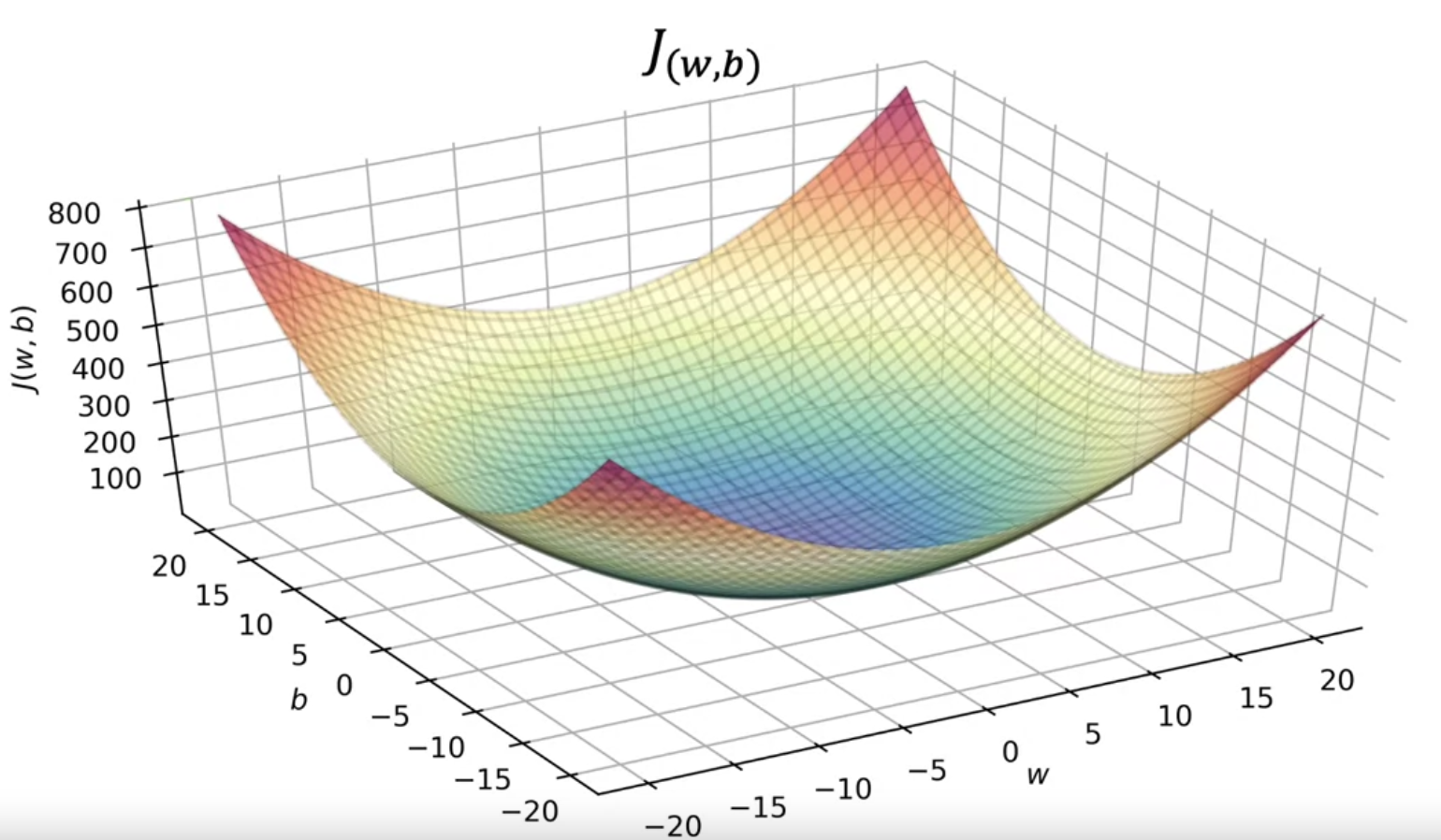
$$ J(w,b) = \frac{1}{2m}\sum_{i=1}^m(f(x^{(i)}) - y^{(i)})^2 $$

代价函数就是衡量模型预测值与训练集实际值之间的偏差，找出合适的 w 和 b，使得这个偏差最小，即 $\underset{w,b}{\text{minimize}} J(w,b)$

# 使用sickit-learn 预测日志数据增长量
from sklearn import linear_model

# 训练数据
# 距离第一天的天数, 是否是周末，数据总量
train_data = [
[1	,0, 54],
[2	,0, 108],
  ...
[22	,0, 80968],
]
# 测试数据
test_data = [
  [76,	1,	148550],
  ...
  [42,	1,	109554],
]
reg = linear_model.LinearRegression()
train_feats = list(map(lambda x: x[0: len(x) - 1],train_data))
train_val = list(map(lambda x: x[-1],train_data))
reg.fit(train_feats, train_val)

print('模型参数 ' + str(reg.coef_))

梯度下降

梯度下降适用所有代价函数

梯度下降背后的思想是：开始时我们随机选择一个参数的组合，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值，但线性回归的代价函数只会有一个最小值

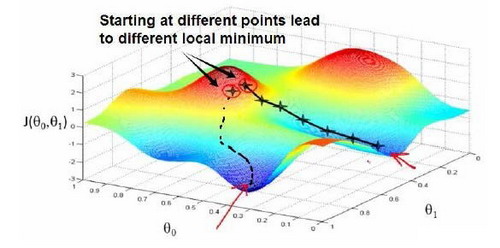
梯度下降算法：

$$ tempw = w - \alpha\frac{\partial}{\partial{w}}J(w,b) = w - \frac{1}{m}\sum_{i=1}^{m}(f(x^{(i)}) - y^{(i)})x_j^{(i)} $$ $$ tempb = b - \alpha\frac{\partial}{\partial{b}}J(w,b) $$

w = tempw
b = tempb

对于多变量的线性回归模型，需要额外对所有的参数进行梯度下降：

$$ w_1 = w_1 - \alpha\frac{\partial}{\partial{w}}J(\vec{w},b) $$ $$ w_2 = w_2 - \alpha\frac{\partial}{\partial{w}}J(\vec{w},b) $$ $$ w_3 = w_3 - \alpha\frac{\partial}{\partial{w}}J(\vec{w},b) $$ $$ [w_1,w_2,w_3,...] = \vec{w} $$

$\alpha$是学习率（learning rate），决定了沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，学习率如果大小了，需要很多步才能到达全局最低点，学习率太大了，可能会越过最低点，甚至可能无法收敛

$\alpha$后面对代价函数的偏导数表示了代价函数在当前取值处的斜率，如果是正斜率，就能得出一个正数，如果是负斜率，就得出负数，这可以使得w，b参数值会向代价函数的最小值的参数值逼近

一个运行良好的梯度下降算法代价函数值应该会随着迭代次数的增加不断收敛到接近局部最小值

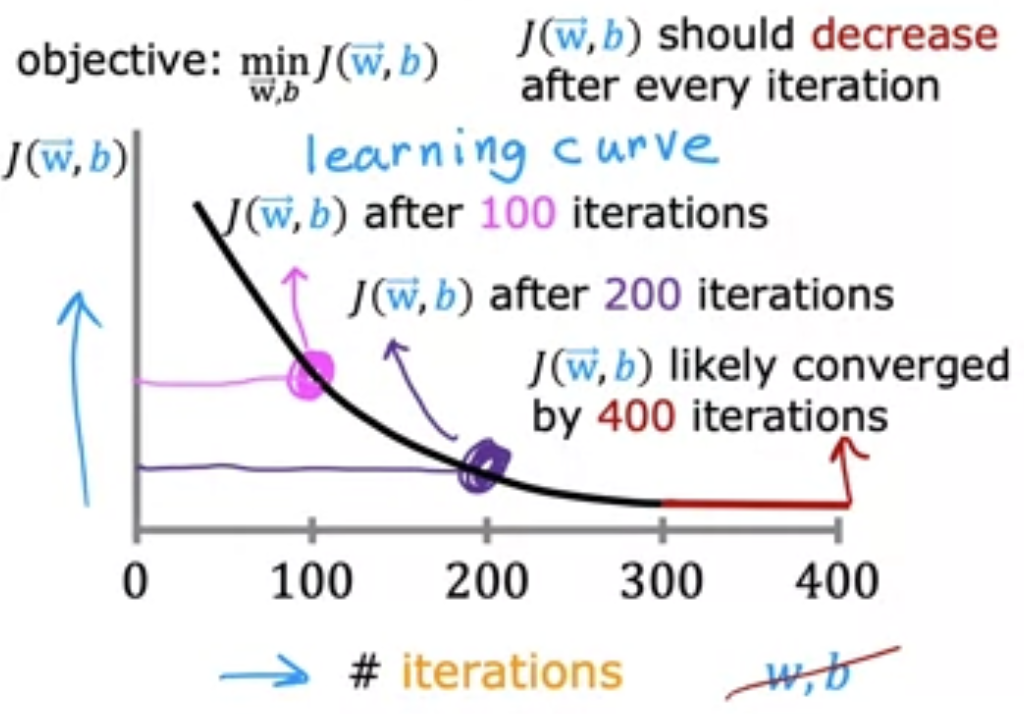
当计算的参数值不再变化时，就代表找到了局部最小值

特征缩放

在面对多维特征问题的时候，要保证这些特征都具有相近的尺度，如所有特征的取值都在0-1之间，这将帮助梯度下降算法更快地收敛

多项式回归

使用线性回归的思路，关键在于为数据添加新的特征，而这些新的特征是原有的特征的多项式组合

逻辑回归

为了对分类问题 $f(\vec{x}) = \vec{w}\cdot\vec{x} + b$ 进行拟合，引入sigmoid函数 $g(z) = \frac{1}{1+e^{-z}}$ 如果把分类问题的参数作为sigmoid函数的参数，就能得到一个输出0 - 1 函数

$$ f(\vec{x}) = \frac{1}{1+e^{-(\vec{w}\cdot\vec{x} + b)}} $$

当$\vec{w}\cdot\vec{x} + b = 0$时，这条线就是决策边界

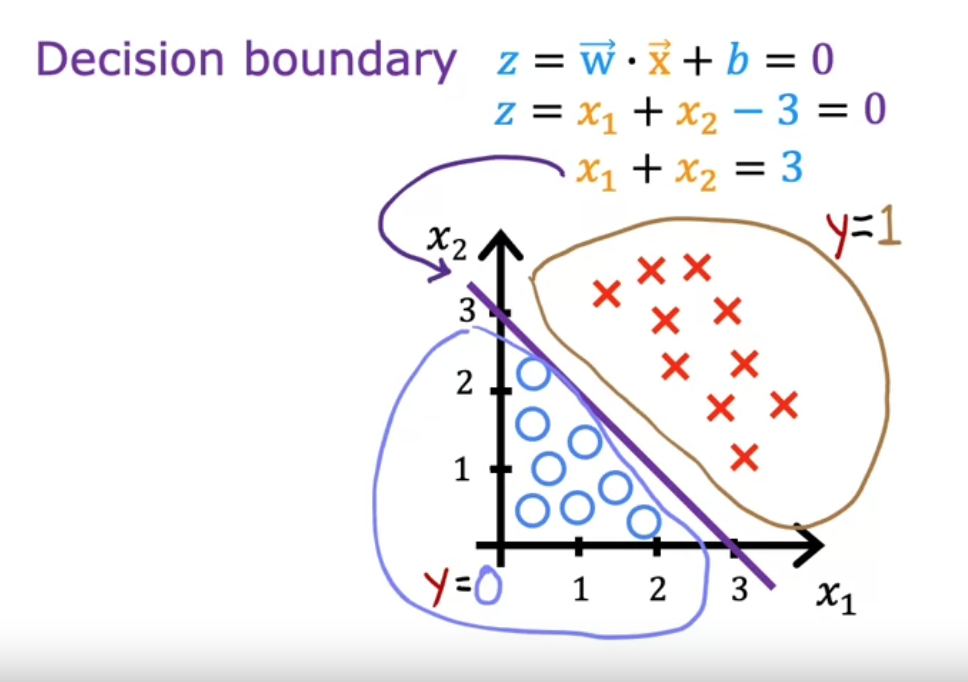
通过找出决策边界，大于这个决策边界的被认为真，否则认为假

逻辑回归使用如下代价函数

$$ J(\vec{w},b) = \frac{1}{m}\sum_{i=1}^m L(f(\vec{x}^{(i)},y^{(i)})) $$

$$ L=\begin{cases}\quad-\log\left(f(\vec{x}^{(i)})\right)&\quad\text{if }y^{(i)}=1\-\log\left(1-f(\vec{x}^{(i)})\right)&\quad\text{if }y^{(i)}=0&\end{cases} $$

损失函数如果预期结果为0 但实际结果为1 则会输出1 否则输出0，也就是充分体现实际结果与预期结果的不同，使得代价函数最小

代价函数都是通过最大似然方法统计数据得出

Softmax回归

Softmax回归是逻辑回归的概括

$$ \begin{array}{rl}{a_{1}=\frac{e^{z_{1}}}{e^{z_{1}}+e^{z_{2}}+\cdots+e^{z_{N}}}}&{{}=P(y=1|\vec{x})}\{\vdots}\{a_{N}=\frac{e^{z_{N}}}{e^{z_{1}}+e^{z_{2}}+\cdots+e^{z_{N}}}}&{{}=P(y=N|\vec{x})}\\end{array} $$ $$ loss(a_1,...,a_N,y)=\begin{cases}-\log a_1&\mathrm{if}y=1\-\log a_2&\mathrm{if}y=2\\vdots\-\log a_N&\mathrm{if}y=N\end{cases} $$

过拟合

解决过拟合：

1. 加入更多的训练数据
2. 进行特征选择
3. 正则化

正则化

修改代价函数：

$$ J(w,b) = \frac{1}{2m}\sum_{i=1}^m(f(x^{(i)}) - y^{(i)})^2 +\frac{\lambda}{2m}\sum_{j=1}^nw_j^2 $$

使得参数 w 越大，代价就越高，这样梯度下降算法就会选择较小的 w ，改善过拟合

如果选择的正则化参数$\lambda$过大，则会把所有的参数都最小化了，但若$\lambda$过小，那就只能得到一条斜率为0的直线

神经网络

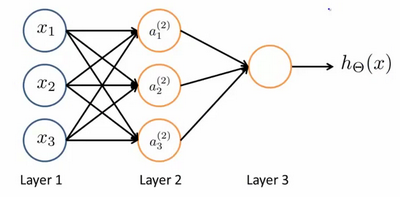
layer1 是输入层，每个节点就是一个特征值

layer2 是隐藏层，每个节点是一个逻辑回归神经元，每个神经元接收上一层的1个或多个特征，产生一个新特征，输出给下一层，接收特征的输入被称为激活，接收特征的输入被称为激活函数，逻辑回归神经元的激活函数是sigmoid函数

layer3 是输出层，其根据上一层输出的所有特征，再输出一个特征值

从左向右每个特征被计算成新特征，这个过程称之为前向传播，Tensorflow使用反向传播算法来替代梯度下降计算出参数

隐藏层中每个神经元处理数据的方式，计算什么特征，都是根据训练数据统计所决定的，而非人工指定

神经网络每一层输出的特征值都比上一层的特征更高级，所以也就能更好地预测数据

# 手动实现前向传播过程
x = np.array([220,200,17])

# 第一层第一个神经元
w1_1 = np.array([1,2])
b1_1 = np.array([-1])
z1_1 = np.dot(w1_1, x) + b1_1
a1_1 = sigmoid(z1_1)
# 第一层第二个神经元
w1_2 = np.array([-3,4])
b1_2 = np.array([-1])
z1_2 = np.dot(w1_2, x) + b1_2
a1_2 = sigmoid(z1_2)
# 第一层第三个神经元
w1_3 = np.array([5,-6])
b1_3 = np.array([-1])
z1_3 = np.dot(w1_3, x) + b1_3
a1_3 = sigmoid(z1_3)
# 第二层
w2_1 = np.array([-7,8,9])
b2_1 = np.array([3])
z2_1 = np.dot(w2_1,a1)+b2_1
a2_1 = sigmoid(z2_1)

结果 = a2_1

激活函数

如果没有激活函数，也就是使用线性激活函数，那么整个神经网络就跟线性回归一样，解决不了更复杂的问题

不同的激活函数会导致神经元输出的模式也不一样

• sigmoid
• 线性激活函数：输入什么就输出什么，等于没有激活函数
• ReLu: 小于0输出0，大于0，输出输入本身

对于输出层，如果解决的是二分类问题，那就需要使用sigmoid，如果解决的是回归问题，输出有负数，选择线性激活函数，输出没有负数，选择ReLu

对于隐藏层，大多数情况下使用的都是ReLu，因为它梯度下降比sigmoid更快

优化算法

• Adam：相比传统的梯度下降算法，这种优化算法使得学习率$a$不是固定的，而是会根据运行情况调大会调小以优化性能

卷积层

卷积层的每个神经单元不会接受上一层的全部特征输入，而是有选择的选择一部分特征，不同神经元选择的特征集合会重叠

评估模型

数据集被划分为训练集跟测试集，一般是七三分

对于回归模型：通过比较不同模型测试集的预测误差的大小，越大代表对未知数据性能越差

预测误差的计算就是原理同线性回归的代价函数：

$$ J(w,b) = \frac{1}{2m}\sum_{i=1}^m(f(x^{(i)}) - y^{(i)})^2 $$

即数据集的预测值与目标值的差累加

更一般的，是把数据集被划分为训练集跟交叉验证集、测试集，一般是六二二分

通过比较不同模型对于验证集的预测误差，选择一个在验证集效果最好的模型，当最终决定使用哪个后模型，使用测试集来展示模型对未知数据的性能

偏差与方差

偏差的含义是模型预测值的期望和真实结果之间的区别，如果偏差为 0，模型给出的估计的就是无偏估计，方差的含义则是模型预测值的方差，也就是预测值本身的波动程度，方差越小意味着模型越有效。

模型的设计追求低偏差，即准确度高，低方差，即比较简单的模型。高偏差意味着过拟合，高方差意味着欠拟合，理想情况下应该选择低偏差与低方差的模型，即在过拟合与欠拟合直接选择

偏差使用训练集计算得到，即对于训练集使用代价函数计算，代价越小，则偏差越高

方差使用验证集计算得到，即对于验证集使用代价函数计算，代价越小，则方差越低

模型验证的任务就是确定模型的复杂度以避免过拟合的发生，选择数据集基本的原则就是确保训练集、验证集和测试集三者两两互不相交，同时保证三个数据集中正例和负例的比例应该大致一致，避免在数据集之间出现不平衡，再在这些数据集上使用Holdout检验或者交叉校验

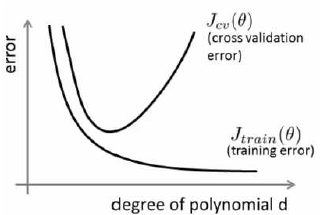
正则化可以用来防止过拟合，如果选择的正则化参数$\lambda$过大，则会把所有的参数都最小化了，这会使得模型欠拟合，而$\lambda$越小，模型就越过拟合

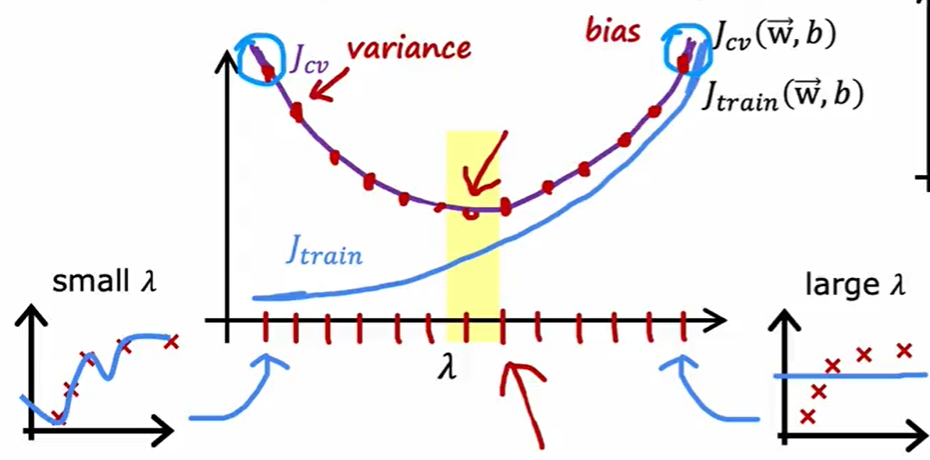
使用学习曲线可以决定是否能通过增加训练数据提升模型效果

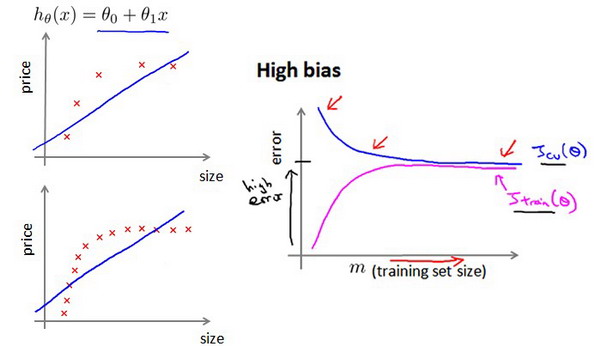
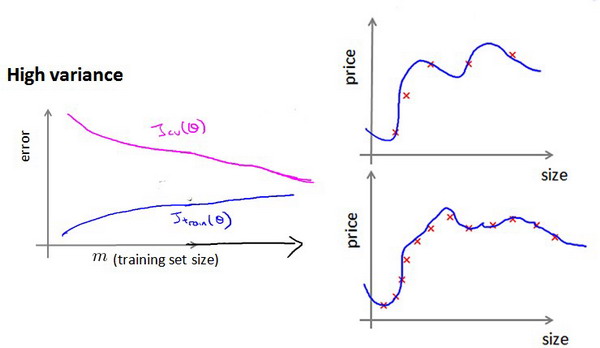
在过拟合的情况下，添加更多的数据能提升模型效果，但在欠拟合的情况下，模型压根就设计的不对，添加再多的数据也无益

• 获得更多的训练样本——解决高方差
• 尝试减少特征的数量——解决高方差
• 尝试获得更多的特征——解决高偏差
• 尝试增加多项式特征——解决高偏差
• 尝试减少正则化程度λ——解决高偏差
• 尝试增加正则化程度λ——解决高方差

较小的神经网络，参数比较少，容易欠拟合。而更大的神经网络，偏差相对会较低，即过拟合，使用正则化可以减少过拟合，但计算代价会越来越高，所以中大型神经网络一般要解决的是高方差的问题，针对不同隐藏层层数的神经网络训练神经网络， 然后选择验证集代价最小的神经网络

增加训练数据

• 数据增强：对已有训练数据进行合理变换，产生新数据
• 数据合成：如通过计算机生成的图像来当做模型的训练数据

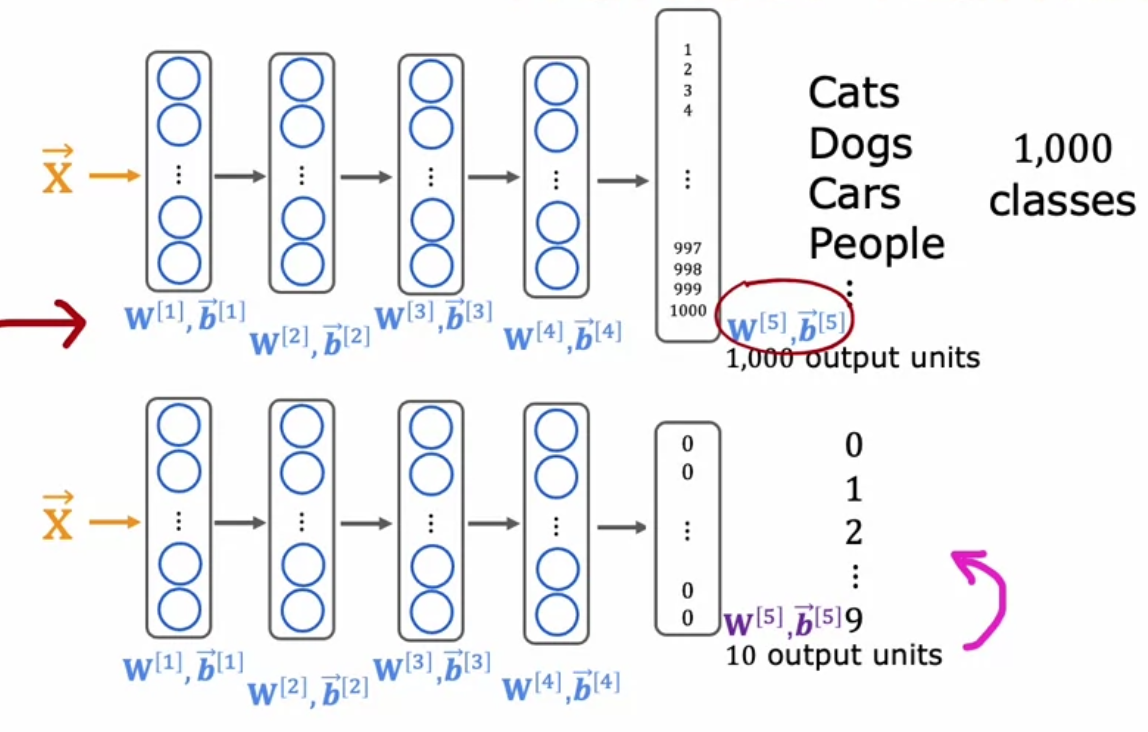
迁移学习

如果要解决的问题没有足够多的训练数据，可以找一个相同任务类型的神经网络，利用其已经训练完成的隐藏层参数，根据需要修改输出层，并输入我们自己的训练数据，对模型进行微调，这样可以有效利用别人已经预训练好的模型来解决我们的问题

异常检测

给定数据集 X，我们假使数据集是正常的，我们希望知道新的数据 是不是异常的，即这个测试数据不属于X的几率如何

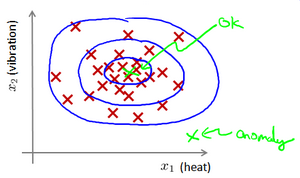
这种方法称为密度估计

$$ if\quad p(x)\begin{cases}<\varepsilon&anomaly\>=\varepsilon&normal&\end{cases} $$

可以用高斯分布来确定已知$x^{(i)}$，求其概率：

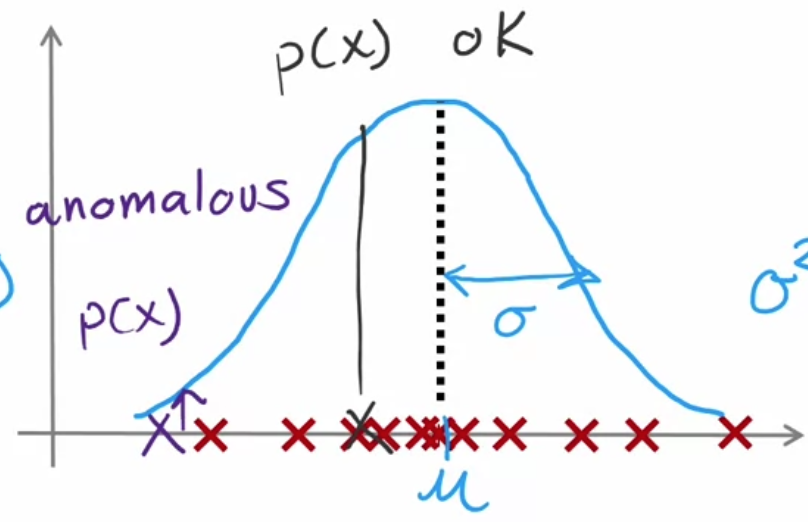
高斯分布由两个参数计算确定：

$$ \mu=\frac1m\sum_{i=1}^mx^{(i)}\ \sigma^2=\frac1m\sum_{i=1}^m(x^{(i)}-\mu)^2 $$

计算一个特征向量出现的概率：

$$ p(\vec{\mathrm{x}})=p(x_1;\mu_1,\sigma_1^2)*p(x_2;\mu_2,\sigma_2^2)*p(x_3;\mu_3,\sigma_3^2)\cdotsp(x_n;\mu_n,\sigma_n^2)\ =\prod_{j=1}^np(x_j;\mu_j,\sigma_j^2) $$

每一个特征都需要计算自己的高斯分布，即自己的$\mu$ $\sigma^2$：

$$ \mu_{j}=\frac{1}{m}\sum_{i=1}^{m}x_{j}^{(i)}\ \sigma_{j}^{2}=\frac{1}{m}\sum_{i=1}^{m}(x_{j}^{(i)}-\mu_{j})^{2} $$

由于异常检测是无监督学习，所以是通过训练集构建密度估计函数，再通过验证集（大量正常数据，少量异常数据）选择合适的$\epsilon$

对比项	异常检测	监督学习
训练数据特征	非常少量的正向类（异常数据 y = 1）, 大量的负向类（y = 0）	同时有大量的正向类和负向类
正向数据占比	许多不同种类的异常，非常难。根据非常少量的异常数据来训练算法。	有足够多的正向类实例，足够用于训练 算法，未来遇到的正向类实例可能与训练集中的非常近似。
挖掘模式	未来遇到的异常可能与已掌握的异常、非常的不同。	找出已存在于训练数据中的模式
场景	欺诈行为检测 生产（例如飞机引擎）检测数据中心的计算机运行状况	邮件过滤器 天气预报 肿瘤分类

异常检测假设特征符合高斯分布，如果数据的分布不是高斯分布，异常检测算法也能够工作，但是最好还是将数据转换成高斯分布，例如使用对数函数 $x = log(x + c)$ 或者 $x = x^c$

我们通常可以通过将一些相关的特征进行组合，来获得一些新的更好的特征（异常数据的该特征值异常地大或小

强化学习

不必告诉算法 每个输入 x 的正确输出 y 是什么，而是要指定一个奖励函数，告诉它何时表现良好，何时表现不佳。 算法的工作是自动弄清楚如何选择好的动作

要解决的问题要多种状态$S(s_1,s2,..,s_n)$ 每个状态都有属于它的奖励$r$，奖励通过奖励函数计算得到：$R(s_i) = r_i$。算法需要根据一个策略$\pi$ 求解当前所处状态应该采取什么行动$a$，即$\pi(s_n) = a$，算法所能最终得到的回报是与折扣因子$\gamma$有关，即最终回报 = $r_1 + \gamma r_2 + \gamma^2 r_3 + ...$

状态操作值函数

$Q(s,a)$返回在状态s下，使用a行动，能获取到的最大回报，并且通过这个行动跟这个状态，后续也是最优解

贝尔曼方程：

$$ Q(s,a)=R(s)+\gamma\max_{a^{\prime}}Q(s^{\prime},a^{\prime}) $$

• $s^{\prime}$ 是采取行动$a$后达到的状态
• $a^{\prime}$ 是要到达$s^{\prime}$所要采取的行动

方程的第一部分也被称为即时奖励，第二部分是从当前状态开始，能得到的最大奖励

这样可以通过贝尔曼方程来创建神经网络的训练数据：

$$ x = (s,a) \ y = R(s)+\gamma\max_{a^{\prime}}Q(s^{\prime},a^{\prime}) $$

让神经网络算出最优的Q函数，这样就可以在当前状态$s$下，应该采取什么行动$a$

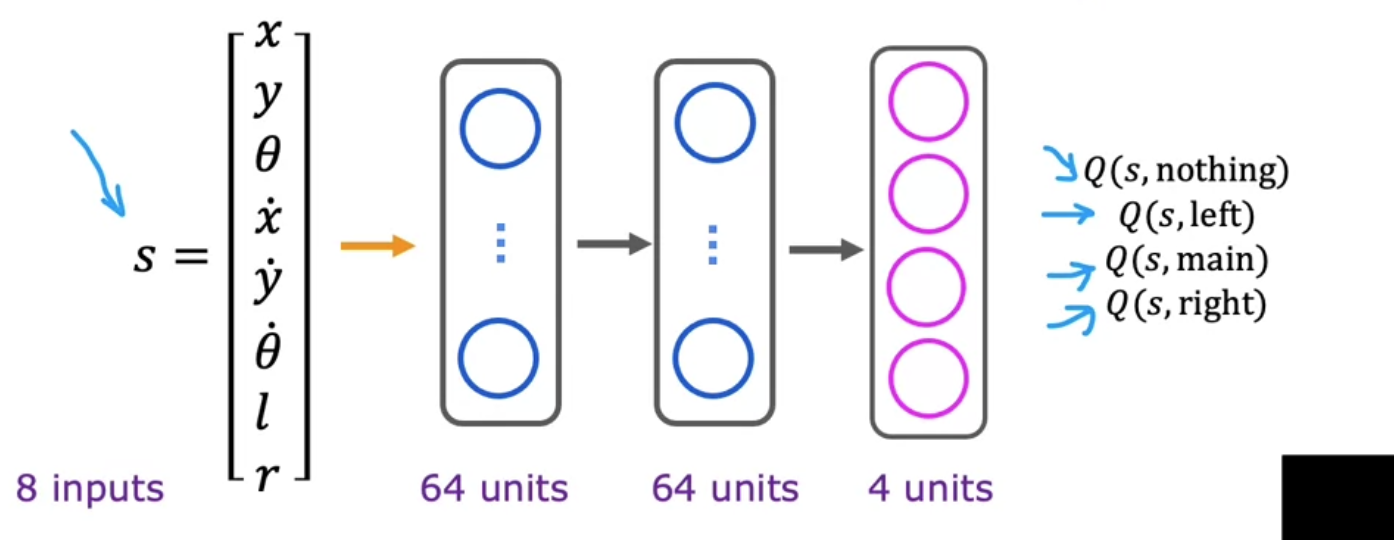
ϵ-贪婪策略

前期收集训练数据时，我们并不知道采取什么行动比较好，一种方式是不管当前状态如何，都采取随机行动。

一种被称为$\epsilon$贪婪策略的方法，定义一个参数$\epsilon$，每次，你有$1-\epsilon$的几率总是选择使得$Q(s,a)$最大的$a$，同时，另外$\epsilon$的几率就是随机做出行动$a$

随机环境

对于某些问题，下一个状态可能是随机的，此时强化学习的目标就从选择最大回报变成使得预期的回报尽可能大

连续状态空间

有些问题的状态取值可能不是离散的，而是一个有连续值的向量

小批量梯度下降

如果训练集数据很多，按照正常的梯度下降，每轮都会把所有训练数据丢到代价函数计算一遍，小批量梯度下降的思想是，每轮梯度下降只取训练数据的一部分，这样可以有效减少计算量。

但这也会导致梯度下降收敛的速度比正常的慢。

软更新

在梯度下降中，为了防止参数更新发生较大变化，我们每次只取一部分新的参数跟大部分老的参数，即

$$ w = 0.01w_{new} + 0.99w\ b = 0.01b_{new} + 0.99b $$